求解給定序列的最長遞增子序列
更新:無代碼,多圖預警!
聲明:非科班算法渣寫的文章,謹慎的看,文章中有任何錯誤請不吝指出,更希望大佬們能提供更多訊息交流,讓我進步。
最長遞增子序列在Virtual DOM算法中的意義
如果了解過ivi/inferno的同學應該知道,在ivi/inferno中Virtual DOM的核心Diff算法中應用到了求解給定序列的最長遞增子序列的算法,用的算法來自: http:// en.wikipedia .org/wiki/L ongest_increasing_subsequence 。當然了,這篇文章不是用來講解這個鏈接中所描述的算法的,而是單純的想要解決:找到給定序列的*所有*最長遞增子序列。
這裡不會講解ivi/inferno 中核心Diff 的實現,但是有些訊息需要做出陳述:新舊children 中的節點有各自的順序,如下圖所示:
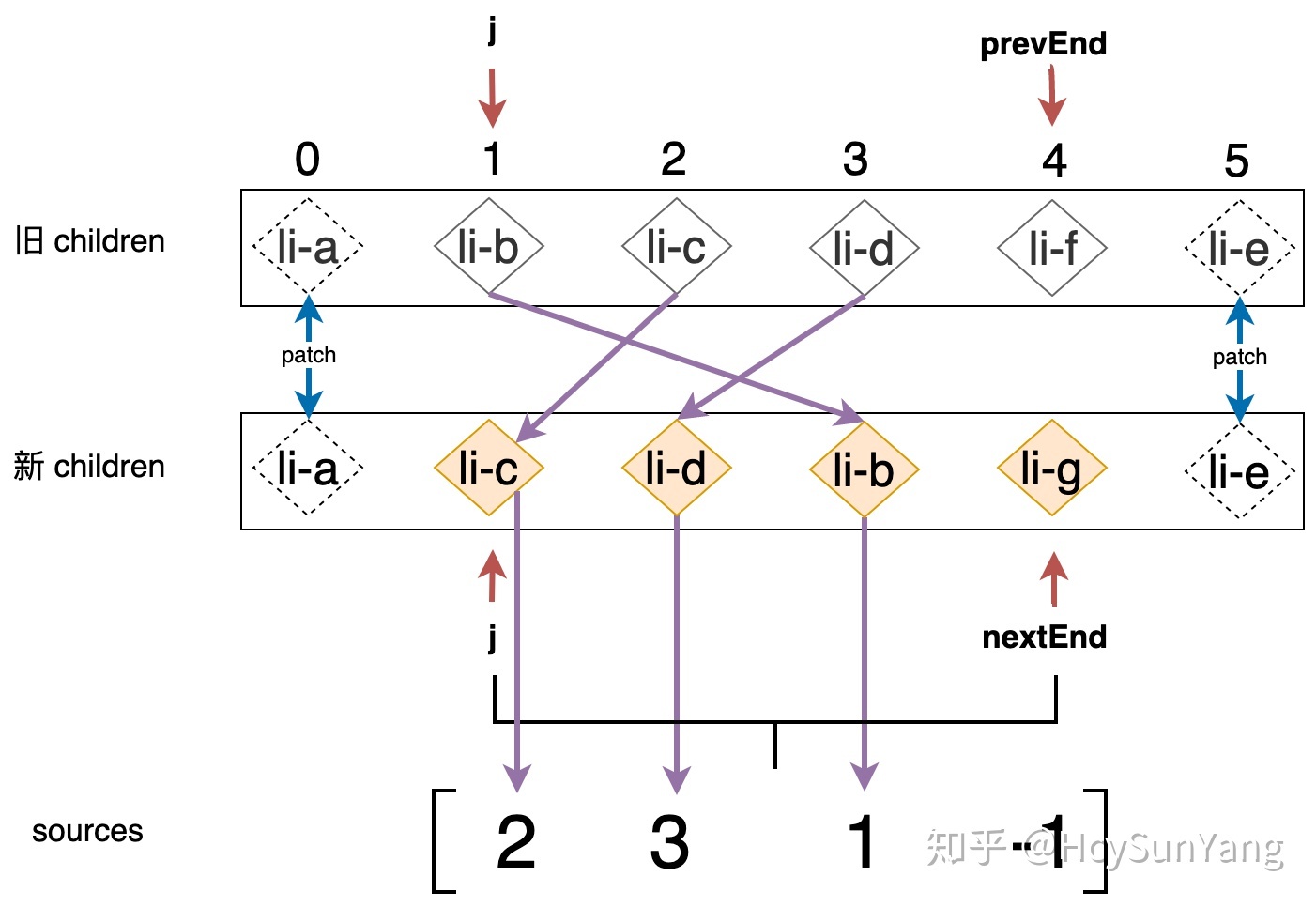
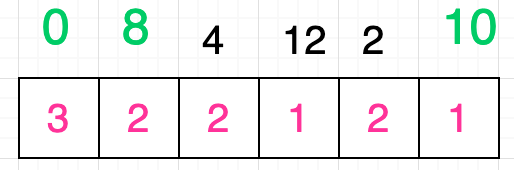
ivi/inferno會構建一個source數組,數組中的值存儲的就是新children中的節點在舊children中的位置,如上圖所示source數組為: [ 2, 3, 1, -1 ] 。接著如果節點需要移動的話,則會把source 數組中的數值作為一個序列,並求解它的最長遞增子序列。對於序列[ 2, 3, 1, -1 ]來說,它的最長遞增子序列就是[ 2, 3 ] ,但實際上我們需要的並不是子序列本身,而是子序列中的元素在source數組中的位置,也就是[ 0, 1 ] 。那麼[ 0, 1 ]的作用是什麼呢?它意味著在新children 中位於第0 和第1 個位置的節點是不需要被移動的,換句話說在上圖中只有li-b 節點是需要被移動的,這種方式能夠保證移動在DOM操作中總是擁有最少的移動次數,但是如何證明它是最少的目前我也不知道,因為我嘗試了很多個案例,發現snabbdom 的移動次數並不會比ivi/inferno 多。所以也希望了解的大佬們指點一下(我單純的指移動DOM 的次數,而非總體的性能)。
求解給定序列的最長遞增子序列
什麼是最長遞增子序列這裡引用一段描述:
在一個給定的數值序列中,找到一個子序列,使得這個子序列元素的數值依次遞增,並且這個子序列的長度盡可能地大。最長遞增子序列中的元素在原序列中不一定是連續的。
不廢話了,設給定的序列如下:
[ 0, 8, 4, 12, 2, 10 ]實際上,這是一個可以利用動態規劃思想求解的問題。動態規劃的思想是將一個大的問題分解成多個小的子問題,並嘗試得到這些子問題的最優解,子問題的最優解有可能會在更大的問題中被利用,這樣通過小問題的最優解最終求得大問題的最優解。那麼對於一個序列而言,它的子問題是什麼呢?很簡單,序列是有長度的,所以我們可以通過序列的長度來劃分子問題,如上序列所示,它有6個元素,即該序列的長度為6 ,所以我們可不可以將這個序列拆解為長度更短的序列呢?並優先求解這些長度更短的序列的最長遞增子序列,進而求得原序列的最長遞增子序列?答案是肯定的,假設我們取出原序列的最後一個數字單獨作為一個序列,那麼該序列就只有一個元素: [ 10 ] ,很顯然這個只有一個元素的序列的長度為1 ,已經不能更短了。那麼序列[ 10 ]的最長遞增子序列是什麼呢?因為只有一個元素,所以毫無遞增可言,但我們需要一個約定: **當一個序列只有一個元素時,我們認為其遞增子序列就是其本身** ,所以序列[ 10 ]的最長遞增子序列也是[ 10 ] ,其長度也是1 。
接著我們將子問題進行擴大,現在我們取出原序列中的最後兩個數字作為一個序列,即[ 2, 10 ] 。對於這個序列而言,我們可以把它看作是由序列[ 2 ]和序列[ 10 ]這兩個序列所組成。並且我們觀察這兩個序列中的數字,發現滿足條件2 < 10 ,這滿足了遞增的要求,所以我們是否可以認為**序列`[ 2, 10 ]`的最長遞增子序列等於序列`[ 2 ]`和序列`[ 10 ]`這兩個序列的遞增子序列“之和”** ?答案是肯定的,而且慶幸的是,我們在上一步中已經求得了序列[ 10 ]的最長遞增子序列的長度是1 ,同時序列[ 2 ]也是一個只有一個元素的序列,所以它的最長遞增子序列也是它本身,長度也是1 ,最後我們將兩者做和,可知序列`[ 2, 10 ]`的最長遞增子序列的長度應該是1 + 1 = 2 。實際上,我們一眼就能夠看得出來序列`[ 2, 10 ]`的最長遞增子序列也是[ 2, 10 ] ,其長度當然為2啦。
為了不過與抽象,我們可以畫出如下圖所示的格子:
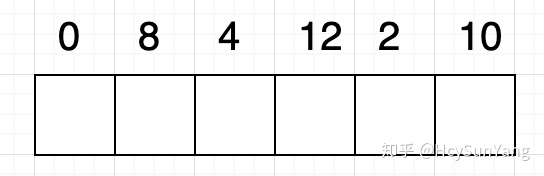
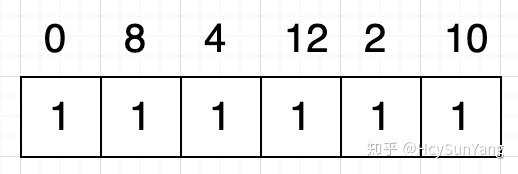
我們為原序列中的每個數字分配一個格子,並為這些格子填充1作為初始值:
根據前面的分析,我們分別求得子問題的序列[ 10 ]和[ 2, 10 ]的最長遞增子序列的長度分別為1和2 ,所以我們修改對應的格子中的值,如下:
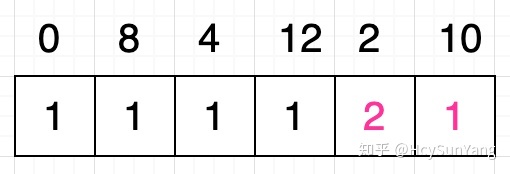
如上圖所示,原序列中數字10對應的格子的值依然是1 ,因為序列[ 10 ]的最長遞增子序列的長度是1 。而原序列中數字2對應的格子的值為2 ,這是因為序列[ 2, 10 ]的最長遞增子序列的長度是2 。所以你應該發現了格子中的值所代表的就是以該格子所對應的數字為開頭的遞增子序列的最大長度。
接下來我們繼續擴大子問題,我們取出原序列中的最後三個數字作為子問題的序列: [ 12, 2, 10 ] 。同樣的,對於這個序列而言,我們可以把它看作是由序列[ 12 ]和序列[ 2, 10 ]這兩個序列所組成的。但是我們發現條件12 < 2並不成立,這說明什麼呢?實際上這說明: **以數字12開頭的遞增子序列的最大長度就等於以數字2開頭的遞增子序列的最大長度** 。這時我們不需要修改原序列中數字12所對應的格子的值,如下圖所示該格子的值仍然是1 :
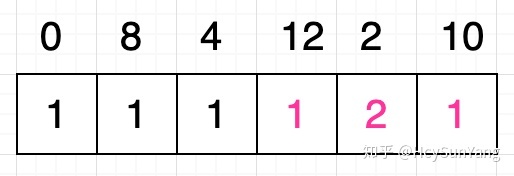
但是這就結束了嗎?還不行,大家思考一下,剛剛我們的判斷條件是12 < 2 ,這當然是不成立的,但大家不要忘了,序列[ 12, 2, 10 ]中數字2的後面還有一個數字10 ,我們是否要繼續判斷條件12 < 10是否成立呢?當然有必要,道理很簡單,假設我們的序列是[ 12, 2, 15 ]的話,你會發現,如果僅僅判斷條件12 < 2是不夠的,雖然數字12不能和數字2構成遞增的關係,但是數字12卻可以和數字15構成遞增的關係,因此我們得出**當填充一個格子的值時,我們應該拿當前格子對應的數字逐個與其後面的所有格子對應的數字進行比較** ,而不能僅僅與緊隨其後的數字作比較。按照這個思路,我們繼續判斷條件12 < 10是否成立,很顯然是不成立的,所以原序列中數字12對應的格子的值仍然不需要改動,依然是1 。
接著我們進一步擴大子問題,現在我們抽取原序列中最後的四個數字作為子問題的序列: [ 4, 12, 2, 10 ] 。還是同樣的思路,我們可以把這個序列看作是由序列[ 4 ]和序列[ 12, 2, 10 ]所組成的,又因為條件4 < 12成立,因此我們可以認為這個序列的最長遞增子序列的長度等於**序列[ 4 ]的最長遞增子序列的長度與以數字12開頭的遞增子序列的最大長度之和** ,序列[ 4 ]的最長遞增子序列的長度很顯然是1 ,而以數字12開頭的遞增子序列的最大長度實際上就是數字12對應的格子中的數值,我們在上一步已經求得這個值是1 ,因此我們修改數字4對應的格子的值為1 + 1 = 2 :
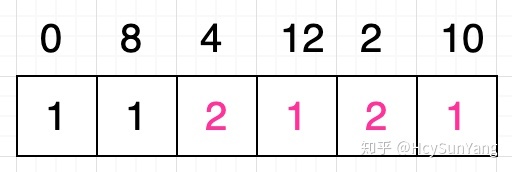
當然了,這同樣還沒有結束,我們還要判斷條件4 < 2和4 < 10是否成立,原因我們在前面已經分析過了。條件4 < 2不成立,所以什麼都不做,但條件4 < 10成立,我們找到數字10對應的格子中的值: 1 ,將這個值加1之後然的值為2 ,這與現在數字4對應的格子中的值相等,所以也不需要改動。
到現在為止,不知道大家發現什麼規律沒有?如何計算一個格子中的值呢?實際很簡單,規則是:
一、拿要填充的格子對應的數字a與其後面的所有格子對應的數字b進行比較,如果條件a < b成立,則用數字b對應格子中的值加1 ,並將結果填充到數字a對應的格子中。
二、只有當計算出來的值大於數字a所對應的格子中的值時,才需要更新該格子中的數值。
有了這兩條規則,我們就很容易填充剩餘格子的值了,接下來我們來填充原序列中數字8所對應的格子的值。按照上面的分析,我們需要判斷四個條件:
1、 8 < 4
2、 8 < 12
3、 8 < 2
4、 8 < 10
- 很顯然條件8 < 4不成立,什麼都不做;
- 條件8 < 12成立,拿出數字12對應格子中的值: 1 ,為這個值再加1得出的值為2 ,大於數字8對應格子的當前值,所以更新該格子的值為2 ;
- 條件8 < 2也不成立,什麼都不做;
- 條件8 < 10成立,拿出數字10對應格子中的值1 ,為這個值再加1得出的值為2 ,不大於數字8所對應格子中的值,所以什麼都不需要做;
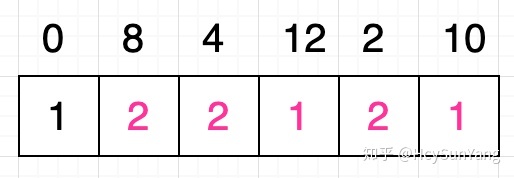
最終我們為數字8所對應的格子填充的值是2 :
現在,就剩下原序列中數字0對應的格子的值還沒有被更新了,按照之前的思路,我們需要判斷的條件如下:
1、 0 < 8
2、 0 < 4
3、 0 < 12
4、 0 < 2
5、 0 < 10
條件0 < 8成立,拿出數字8對應格子中的值: 2 ,為這個值再加1得出的值為3 ,大於數字0對應格子的當前值,所以更新該格子的值為3 。重複執行上面介紹的步驟,最終原序列中數字0對應格子的值就是3 :
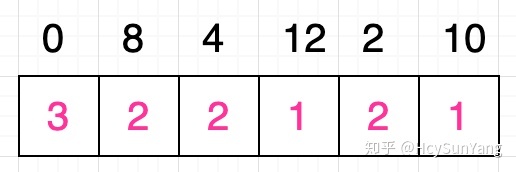
如上圖所示,現在所有格子的值都已經更新完畢,接下來我們要做的就是根據這些值,找到整個序列的最長遞增子序列。那麼應該如何尋找呢?很簡單,實際上這些格子中的最大值就代表了整個序列的遞增子序列的最大長度,上圖中數字0對應格子的值為3 ,是最大值,因此原序列的最長遞增子序列一定是以數字0開頭的:
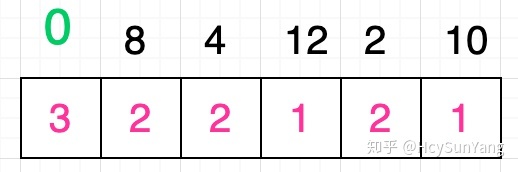
接著你需要在該值為3的格子後面的所有格子中尋找數值等於2的格子,你發現,有三個格子滿足條件,分別是原序列中數字8 、 4 、 2所對應的格子。假設你選取的是數字4 :
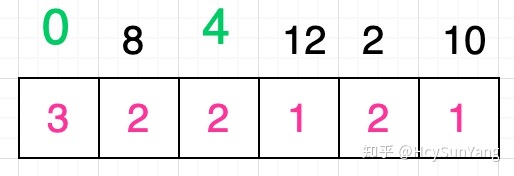
同樣的,你需要繼續在數字4對應的格子後面的所有格子中尋找到數值為1的格子,你發現有兩個格子是滿足條件的,分別是原序列中數字12和數字10所對應的格子,我們再次隨機選取一個值,假設我們選擇的是數字10 :
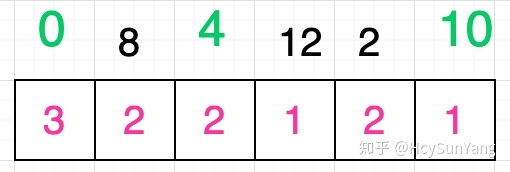
由於格子中的最小值就是數字1 ,因此我們不需要繼續尋找了。觀察上圖可以發現,我們選取出來的三個數字其實就是原序列的最長遞增子序列: [ 0, 4, 10 ] 。當然,你可能已經發現了,答案並非只有一個,例如:
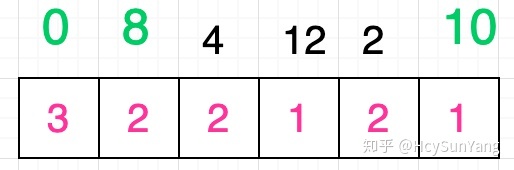
關鍵在於,有三個格子的數值是`2`,因此你可以有三種選擇:
- [ 0, 8 ]
- [ 0, 4 ]
- [ 0, 2 ]
當你選擇的是[ 0, 8 ]時,又因為數字8對應的格子後面的格子中,有兩個數值為1的格子可供選擇,所以你還有兩種選擇:
- [ 0, 8, 12 ]
- [ 0, 8, 10 ]
同樣的,如果你選擇的是[ 0, 4 ] ,也有兩個選擇:
- [ 0, 4, 12 ]
- [ 0, 4, 10 ]
但當你選擇[ 0, 2 ]時,你就只有一個選擇:
- [ 0, 2, 10 ]
這是因為數字2所對應的格子後面,只有一個格子的數值是1 ,即數字10所對應的那個格子,因此你只有一種選擇。換句話說當你選擇[ 0, 2 ]時,即使數字12對應的格子的值也是1 ,你也不能選擇它,因為數字12對應的格子在數字2對應的格子的前面。
以上,就是我們求得給定序列的**所有**最長遞增子序列的算法。
代碼可以在這裡看這裡:
這是利用上面的思路,計算一個最長遞增子序列的實現。要求解全部的話也可以,我先把文章發了,後面會更新。