隨著移動互聯網的一路高歌，越來越多的APP 不滿足系統原生的UI 體系。開啟了各種花式的玩法。
早幾年ReactNative，Weex 等，企圖嘗試讓系統組件可以像瀏覽器一樣動態加載，從而提高發版本的效率。更早幾年還有一眾通過在系統Webview 基礎上面搭建起來的動態化方案，包括當下諸多的小程序平台等。
Flutter 的發布彷彿給業界帶來一絲新的生機，通過Skia 渲染器完美的保證了在諸多平台渲染的一致性。但也帶來專屬於Flutter 本身的一些問題。不過多的討論關於Flutter 本身，這裡只談關於Skia 和矢量渲染技術中屬於我的理解。

首先要承認我是徹徹底底的標題黨。目前為止我通過官方的編譯選項來對Skia 進行編譯裁剪，二進制體積依舊很大。而我的目標就是把Css 和排版還有渲染器整體做到1.5MB 以內，如果選用合理小巧的JS 引擎整體控制在2MB 到2.5MB 左右。

所以如何把Skia 裁剪到！ ！

目前渲染器已經基本完成，關鍵節點的性能測試和Skia 處於同一水平（甚至還要好一些）。但是體積只有Skia 體積（瘋狂裁剪後）的1/8。大概是多大？ 580KB(x86-64 下構建的產物，Android Armv7a 下還要小許多)。在這基礎上又添加了對複雜文本的排版功能，這部分依賴Freetype（解析字體文件的開源庫）和Harfbuzz（對字模整形的開源庫）還有文本的排版引擎，帶上這部分功能體積會大一些（目前為止Skia 還不具備複雜文本排版能力）。

本文希望可以通過簡單通俗的語言和大家探討渲染器背後的核心技術，如果你也有類似的需求希望能給到足夠的啟發。

關於矢量渲染器

矢量渲染器作為現代UI 的核心支撐模塊，常常被作為內嵌在操作系統內的圖形子系統的一部分提供給上層開發者。比如Windows 下的GDI/GDI+/Direct2D，Android 下的Skia/HWUI （HWUI 對一些複雜多邊形的處理依舊依賴Skia 的軟繪製，所以不能算完備的矢量渲染器），MacosX/iOS 內置的CoreGraphics，Linux 下的Cario 渲染器。

同樣其他的跨平台的庫，比如QT 就自己實現了矢量渲染器，這樣可以在不同平台下擁有統一的渲染效果。 Flutter，Chrome 和Android 採用同樣的Skia渲染器來完成跨平台的能力。 ?所以要想在不同平台擁有比較好的渲染一致性，剝離對系統提供渲染器的依賴是很重要的一步。

同樣行業出現了一些類似於包括NanoVG 在內的一些渲染器，此類渲染器都採用了模板掩碼的一種特殊技法（Opengl 紅寶書中提到的）來解決複雜多邊形的繪製問題，巧妙的規避了複雜的幾何運算。但是天下沒有免費的午餐，它同樣也會帶來相對應的性能問題。而且天花板很低，後續優化幾乎無從下手。對於遊戲這類的場景偶爾需要顯示一些面板來說無可厚非，但是對於傳統的界面程序還是顯得捉襟見肘。

前言

在探討之前我覺得有必要定義一下“渲染”這個詞。這個詞在目前互聯網技術上面有諸多含義，帶有一定的迷惑性。下文所有提及的“渲染”都和計算機圖形學中“渲染”擁有同樣的含義，指的是把特定的像素填充對應的顏色，以及圍繞這一目的的相關算法。

鳥瞰渲染器全貌

時至今日Google 甚至微軟的諸多產品都採用Skia 作為核心渲染組件。包括但是不限於Android、Chrome、Flutter、Xamarin 等等。不得不說這是一個偉大的技術產品。

渲染器本身是一個極其複雜的程序，就拿Skia 來說核心側有超過80w 行的代碼。如果算上第三方庫甚至達到了驚人的150w 到200w 行之巨。即使構造的這個輕量的渲染器項目也有超過25w行的代碼（剔除第三方庫，比如圖片編解碼、字體解析、XML 加載庫等等。仍然還有超過13w行的核心代碼）。

這麼複雜的項目我打算從以下幾個方向來依次闡述它的核心技術：

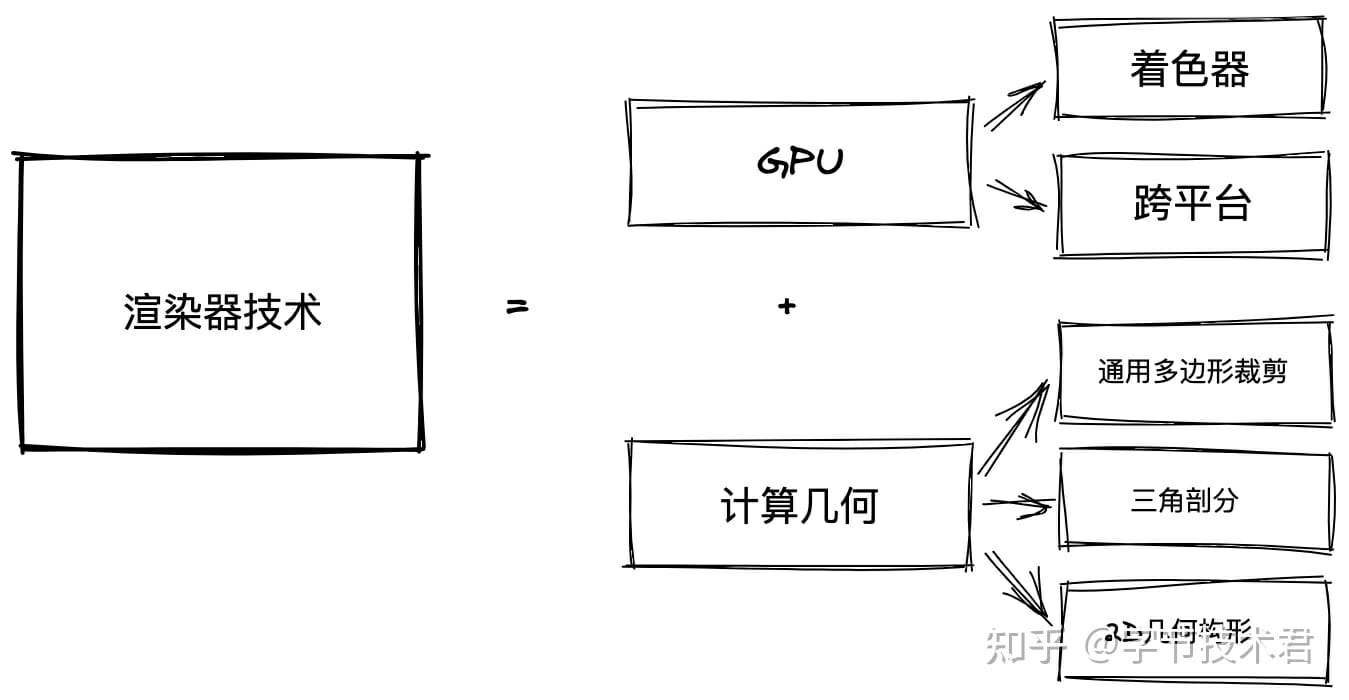
GPU 硬件加速能力的抽象

硬件加速之所以快，在於運算單元多，並行能力強。同樣也帶來一些限制，參與運算的數據必須符合併行計算的要求。下圖描述了大致的流程。

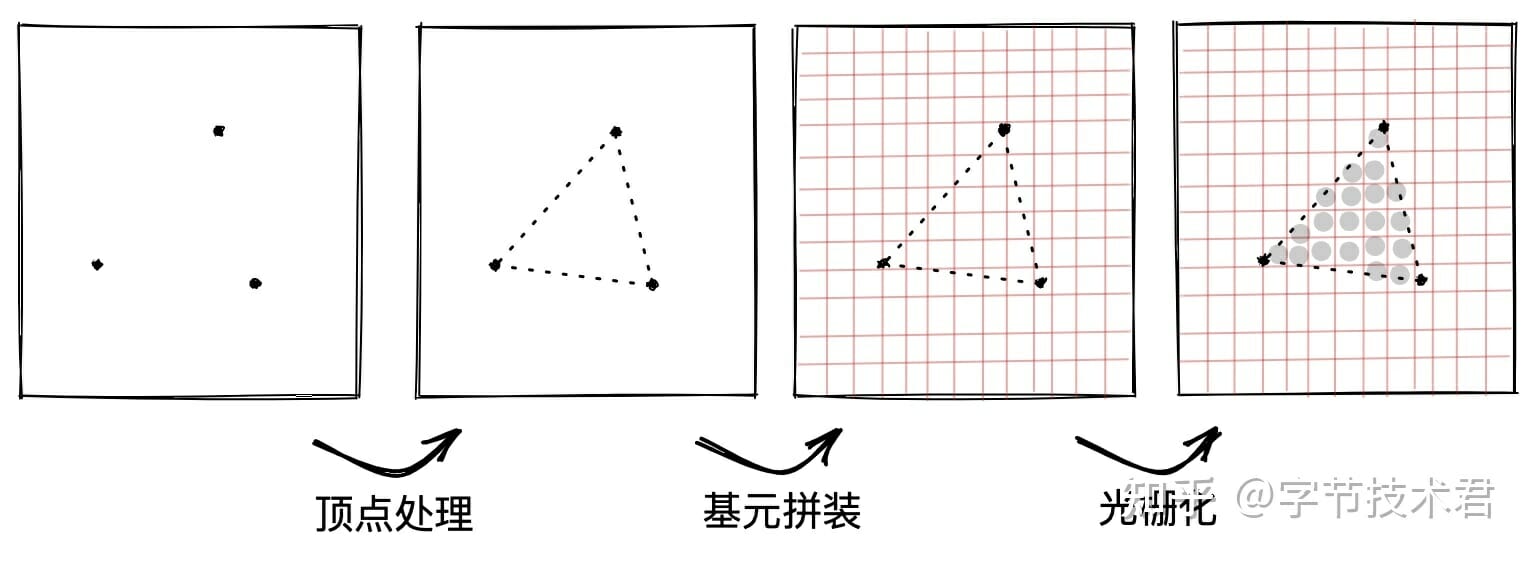
渲染抽象層的設計

目前消費電子設備基本都配備了硬件顯卡，但是很不湊巧主流設備中的顯卡驅動存在較大的差異。因此想要構建完善的硬件加速渲染器，對不同廠商的GPU 驅動做一層抽像是非常有必要。

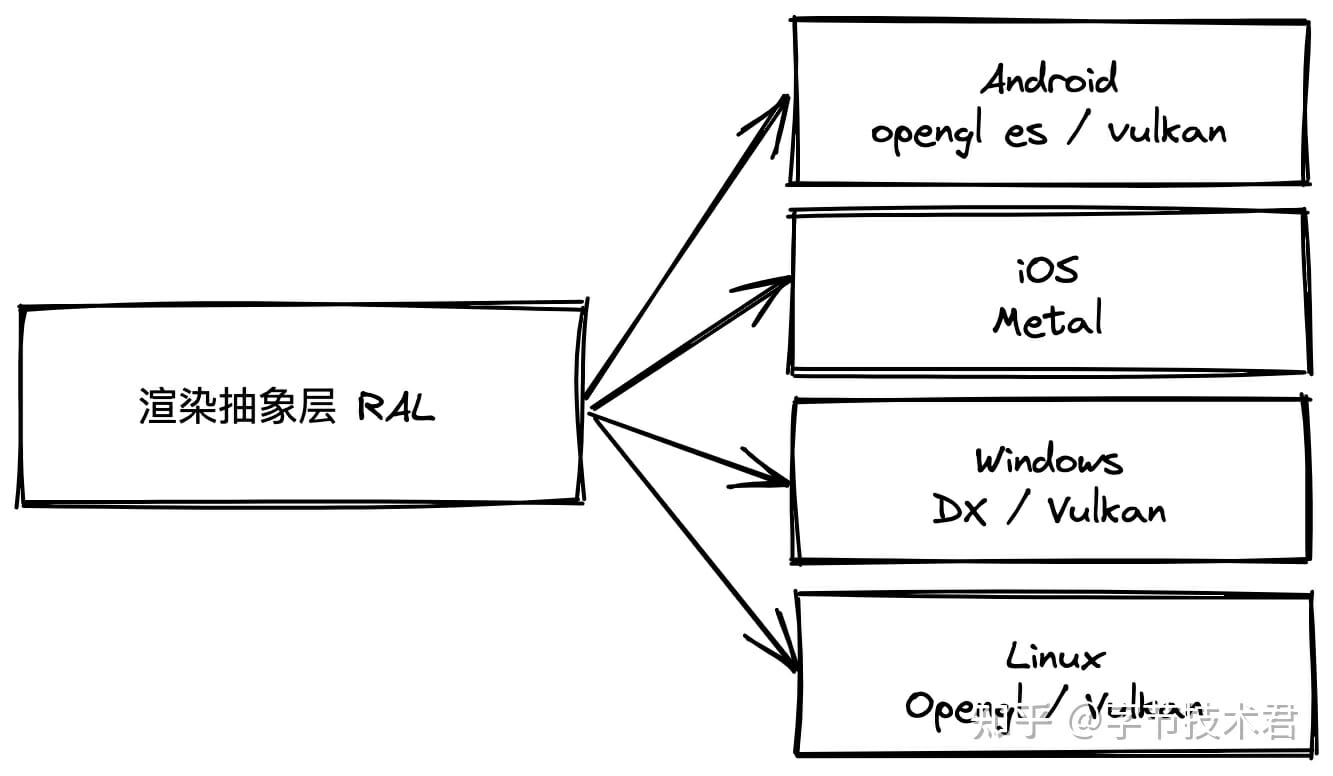
這裡叫RAL（Render Adapter Layer）這只是一個名稱。在遊戲引擎行業中大家更習慣於叫它RHI（RHI 一般還涉及線程和異步的相關策略），詳細可以參考Unreal 的設計。

那麼RAL 到底涉及哪些東西？這就要說到顯卡的差異了，就目前來說主流的圖形技術在所有顯卡中都是相通的。顯卡核心組成部件都類似（高級顯卡存在一些新的著色器流程，暫時我們不會用到）。只是驅動在所在的平台存在差異，也就是顯卡功能性的描述接口存在差異。這部分差異主要存在於2 個方面（當然還存在一些細微細節不一樣，比如窗口坐標系和NDC 的差異，紋理採樣坐標系的差異）。

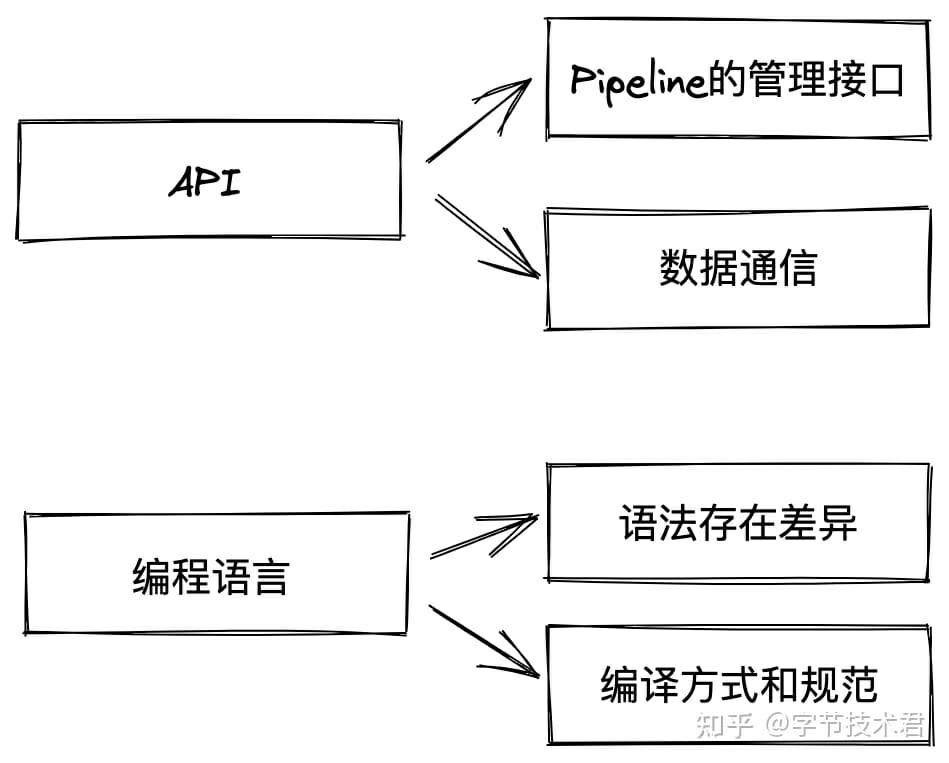
其中API 的差異可以通過對驅動接口的包裝來抹平（有點繁瑣），編程語言就相對來說非常麻煩了。 Skia 內部內置了自己的一套顯卡編程語言叫SKSL，可惜文檔比較少。為了達到縮減包體積的效果，設計了一套自己的編程語言。我管它叫RSL。

設計一套新的Shader 編程語言

為什麼要設計一套新的編程語言和語法？為什麼不直接使用glsl 的語法？

這裡有2 方面的思考（主要為了方便我實現編譯器或者叫轉化器）：

• 在這之前我嘗試讓OpenglES 運行在iOS 的Metal 之上（小遊戲引擎的內核項目），手寫過glsl 的編譯器。用來轉化到Metal 的MSL 語法之上。由於glsl 的Spec 文檔有點多而且複雜，為了測試編譯器的穩定性，抓取了ShaderToy（一個交流webgl shader 的網站）1w5 千個左右的shader 進行測試。語法分析通過率只有95%多點，總有一些我沒有考慮到語法。所以說還是不太穩定，工作量有點大。
• glsl 規範比較老，缺乏語義的支持。
• 應該還有其他的理由，比如我自己設計的語法。但凡有不太容易實現的部分，我可以選擇剔除掉。

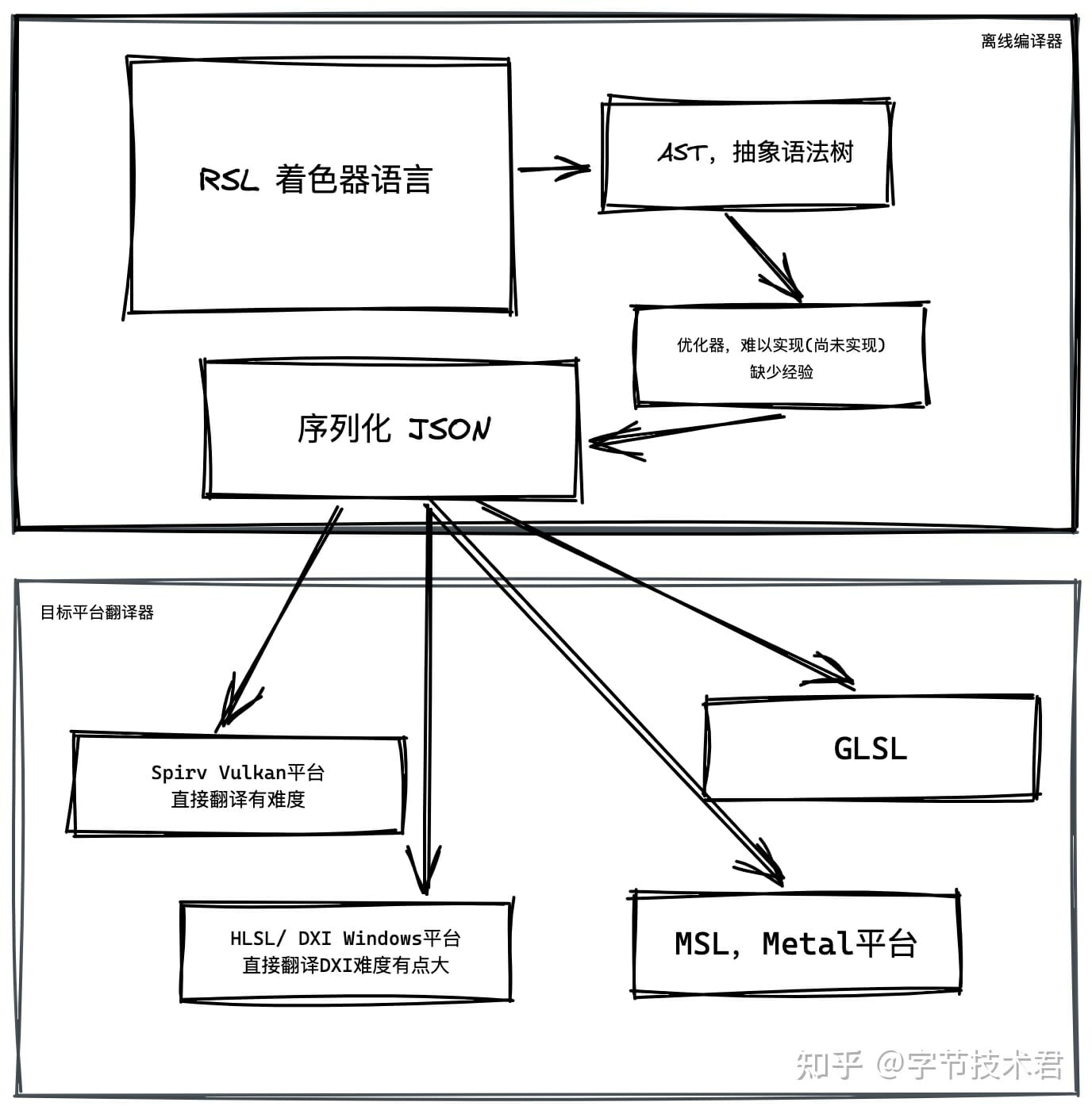
為了縮小包體積，我嘗試把Shader 的編譯拆分成離線和在線兩個端。和大多編譯器的項目類似，或許他們都管這叫編譯前端和後端。

離線端現在開源的編譯器項目很多，比如Flex 和Bison 很容易就可以構建出離線端。理論上應該對AST 進行優化操作，奈何我本人對優化算法知之甚少。所以目前還沒有實現任何優化相關的部分。最後對AST 進行序列化，也可以稍微做點處理，一切以方便設備端翻譯工作為目的，然後就可以內嵌或者動態下發到目標端上面了。

在線端目前主要搞定了OpenglES 和Metal 兩個主力平台，Vulkan 正在進行中。

在開源中找找答案

Bgfx

bgfx 是一套對顯卡接口的抽象，相對來說比較全面。它通過內置一個開源的C 語言宏處理器的方式，來利用宏展開的特性把自定義的Shader 語法實時翻譯成目標平台的語法。我沒有選擇它的原因是我不喜歡它對Shader 語法的處理方式，就其本身來說是一個非常優秀的項目。

Spirv

在Spirv 字節碼（Vulkan 支持的Shader 字節碼，不是編程語言）慢慢變成顯卡跨平台字節碼的事實標准後，行業也出現了一些利用Spirv 來進行Shader 轉化的項目。

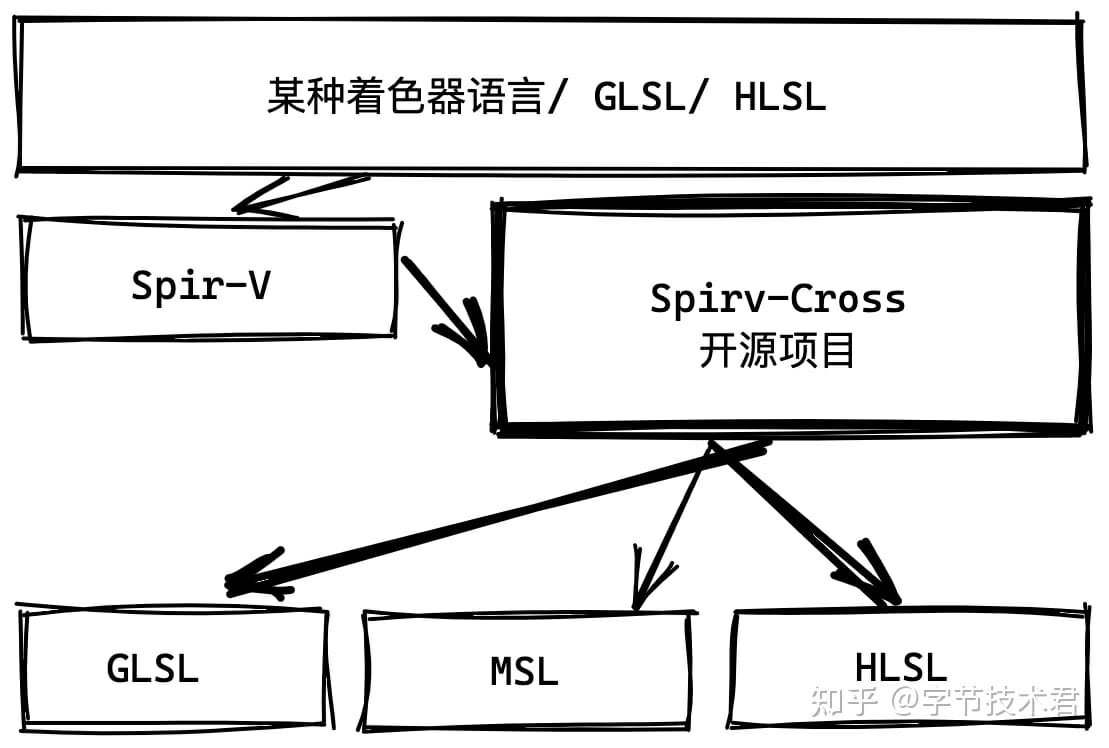
我有想過把RSL 的實現換成微軟的HLSL 實現，這樣我就可以不用維護RSL 的編譯器。同時還能享受微軟HLSL 編譯器強大的優化能力。實際上我也確實這麼做了，但是這樣會明顯增加包體積（會增加十幾MB，我實在沒有辦法忍受把這麼一個巨無霸塞進去）。所以目前也是只是對內置的Shader 在離線編譯的時候會使用這個編譯方案。如果需要動態下發還是保留RSL 的方式，互相補充。這也是目前能找到的最好最穩定的辦法，重點是不增加二進制體積。

幾何

從這一節開始涉及渲染器最為核心的靈魂，數學是一切魔法的開始。

三角形和三角剖分

在圖形學中三角形的重要性已經沒有必要去描述了。它的質性簡單，可以讓顯卡的插值器更加簡單高效的工作。試想一下如果顯卡支持的不是三角形而是四邊形，那麼由四個頂點很有可能不共面，這就會出現很複雜的情況了，而三角形則不會出現這個問題。

如果只能渲染三角形那就太單調啦，實際情況中通常需要把多邊形剖分成一組三角形的網格，我們管這個網格叫Mesh。只有得到了Mesh 後才能提交給GPU 並行計算。我們管這個過程叫三角剖分，可見三角剖分是聯繫複雜多邊形和三角形之間的橋樑。

複雜的多邊形

如何定義多邊形？在計算幾何裡面也是一個比較麻煩的問題，常見的多邊形可以是下圖這樣的。

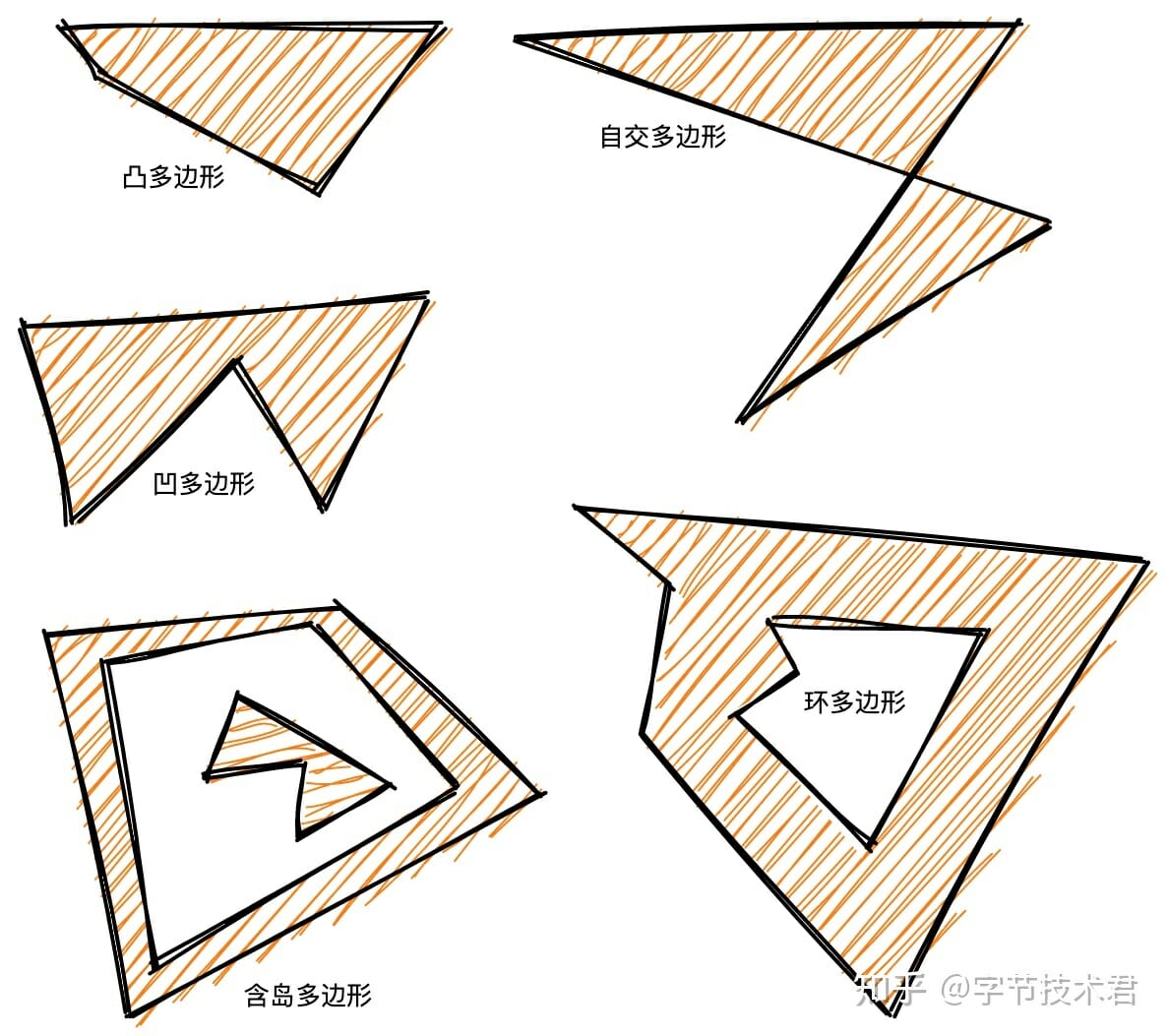
這些還是多邊形家族中一小部分。當我們說起多邊形，可能第一印像想起的是矩形，矩形是最簡單的凸多邊形，它也存在一些非常重要的性質。 region 這類數據結構在表示區域的時候，會使用多個不相交的矩形來進行數學表達。如果存在相交的情況可以利用線掃描快速剔除重疊的區域。這就是利用了他足夠簡單的特性，運算速度可以飛快。

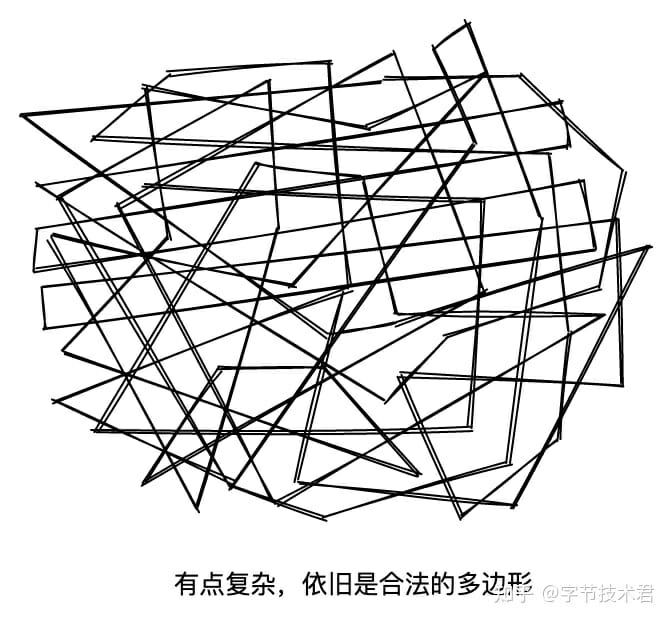
如上圖所示，看起來雜亂無章實際上也是一個合法的多邊形。這樣的多邊形也應該被算法正確的處理，比如三角化，甚至做一些布爾運算。

多邊形規範

在圖形學中會使用一些關鍵點序列來描述一個多邊形。通常認為沿著關鍵點序列的順序行走，左手邊代表多邊形的內部，相反右手邊代表多邊形的外部。

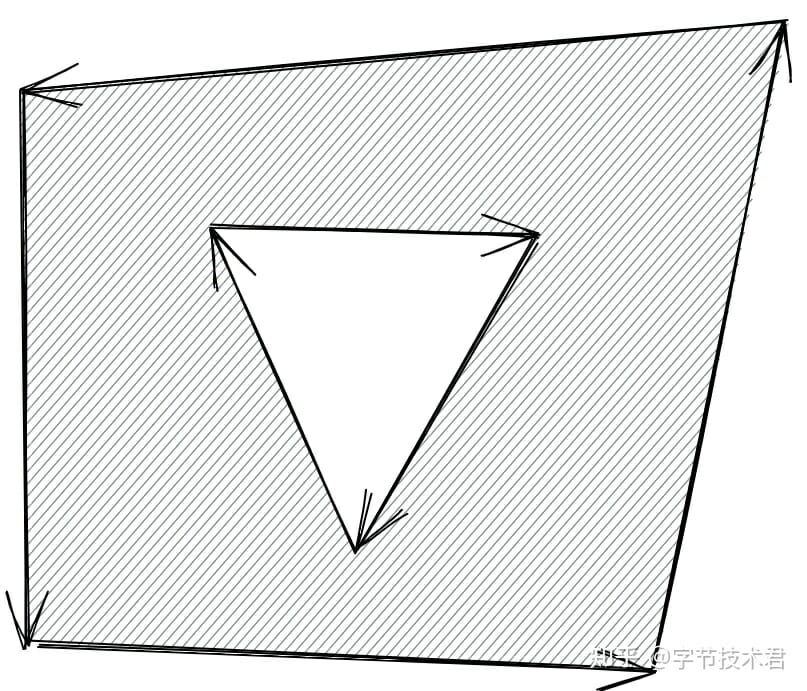
如上圖陰影部分代表多邊形的區域，它有內外2 個順序相反的多邊形組成。按照前文的定義很容易就可以得到多邊形的區域，同樣也很容易用程序的方式存儲這個多邊形。它還是比較簡單的，實際運算過程中允許多邊形存在父子關係（用來存儲含島多邊形），也允許一個多邊形的定義存在多個不連通分量，從這個角度多邊形是典型的遞歸定義。

對上面這個多邊形進行硬件加速渲染，就需要對它進行三角剖分，如下圖紅色虛線構成的三角形網格。

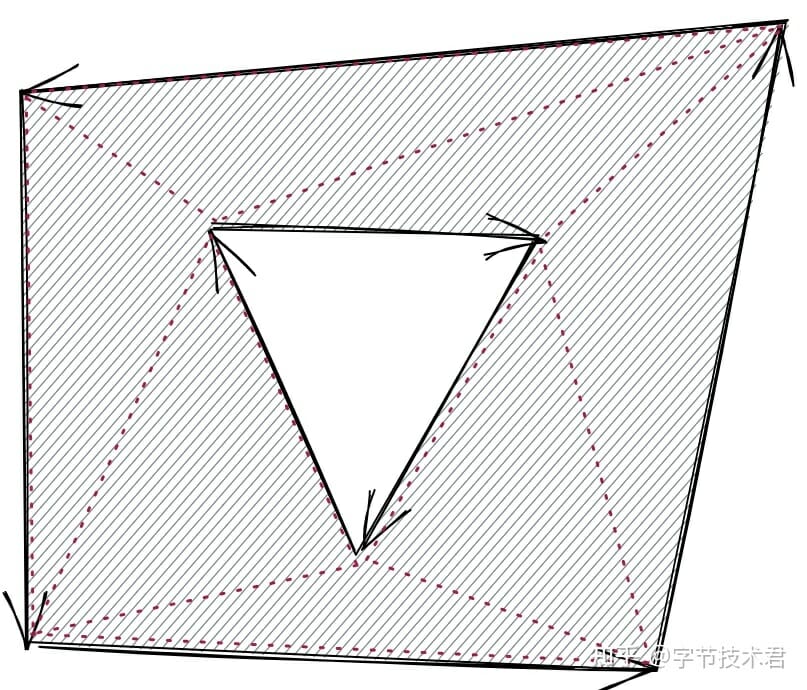
這裡有一個問題，類似於圓這樣的“多邊形”應該如何處理？對於曲線需要先進行離散化，一般在處理的過程中會傳遞一個忍受值，當離散相鄰的兩個點之間的距離小於忍受值就不在進行細分了。所以曲線可以看成由許許多多的“短”的線段圍成的多邊形。

時至今日三角剖分算法已經是計算機圖形學中一個成熟的話題了。常見的三角剖分算法比如“Monotone”、“EarCut” 等等。其中Mapbox（一家專注以地圖渲染的公司）就開源了一個袖珍精巧的基於“Earcut”的剖分算法。還有一些剖分算法對生成的三角形的形狀具有有一定的約束，比如“符合德勞內的三角剖分算法”。在工業領域當然不希望剖分出來的三角形又長又細。因為這樣用做零件加工、存儲和運輸都十分不方便。

畫一條直線

有了前文的理論支持，現在開始面對一些實際的問題吧，比如從畫一條直線開始。

在幾何中只需要2 個端點的坐標就可以描述一條線，從數學的角度看線是沒有寬度的。如果我們需要繪製一條有寬度的線就需要把線轉化成面（或者是一個矩形）。

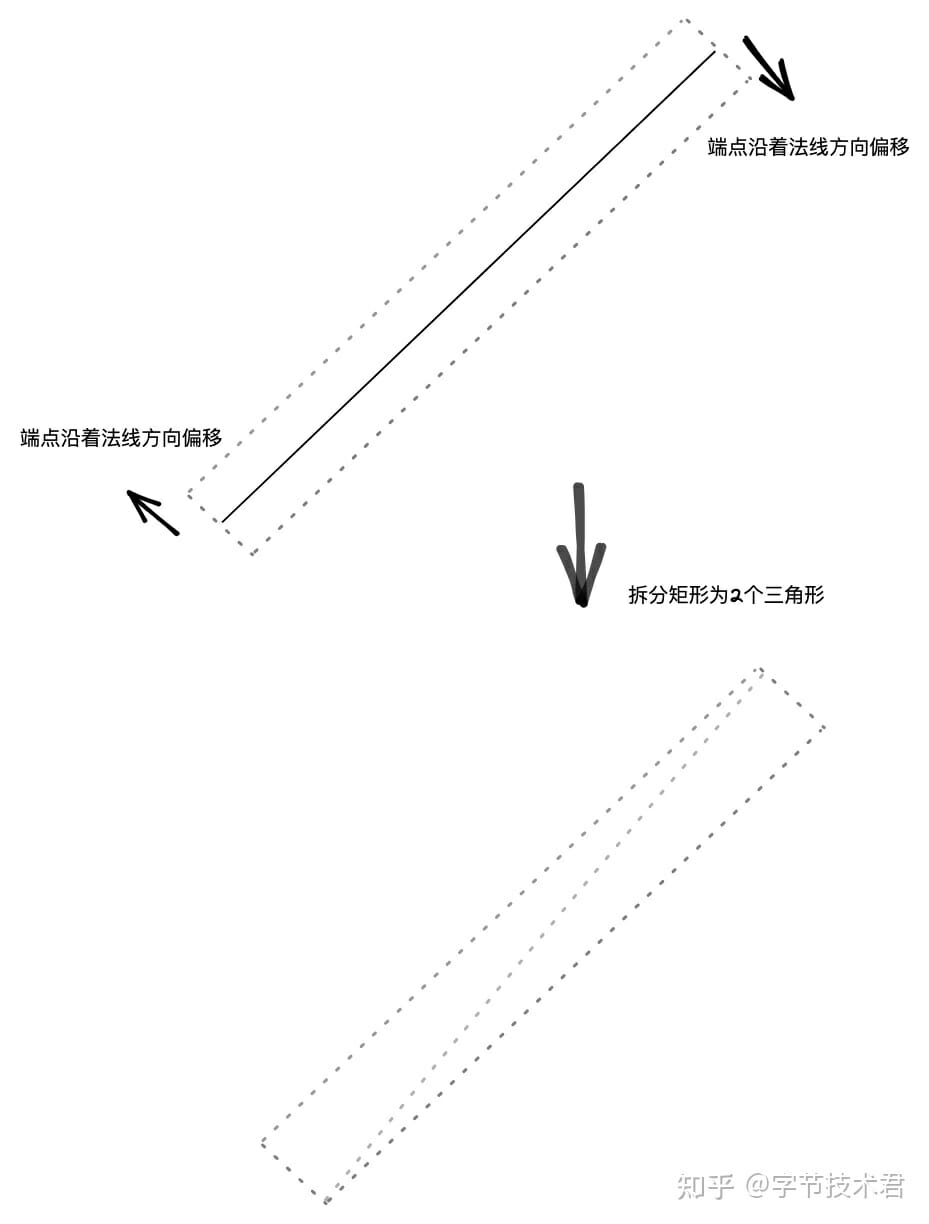
利用給定的線寬並沿著直線的法線方向（一條直線有兩個法線方向，互為相反向量）進行偏移。就可以得到一個矩形，對這個矩形進行剖分就可以得到由2 個三角形組成的三角網格。 GPU 可以高效繪製這個網格，用以表示這條有寬度的線。

畫一條折線

稍微複雜一些，但是原理和繪製一條直線基本類似。

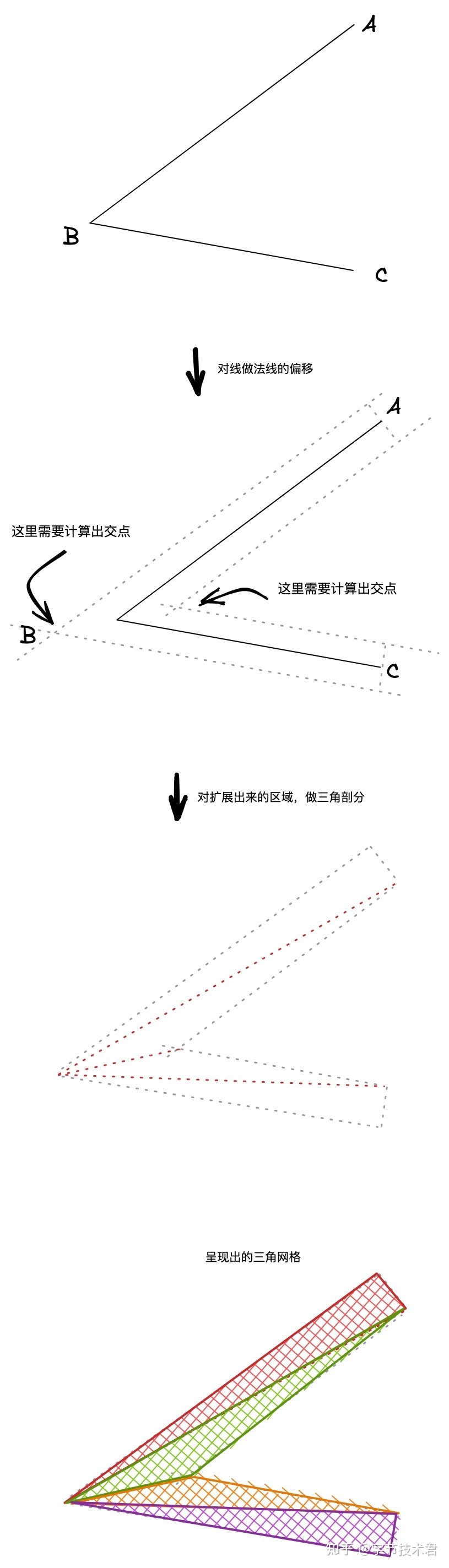
如上圖所示，最後得到了4 個三角形的網格，分別是在渲染器中，可能還需要指定線的端點和交點的樣式。比如圓角端點，交點的長度限制等等。這些都可以用計算幾何的方式得到，這裡就不做過多的介紹。

貝塞爾曲線

前面我們探討了一些基礎的幾何知識。已經可以從面（也就是多邊形）和線（甚至是曲線）得到對應的三角形網格。程序可以構建一些簡單的多邊形（比如矩形，圓形，橢圓等等）然後把這些多邊形轉化成三角形網格，但是如果想要繪製下圖圖形則會發現有些難度。

難度體現在如何得到圖形的輪廓，也就是如何構建或者優雅的描述這樣一個複雜的多邊形。就像美術從業人員會用Photoshop 這類產品做產品的原型設計，大多會用到一個叫“鋼筆工具”的繪圖功能。它通過使用Skia 的SkPath 類的功能就和“鋼筆工具”類似。

具體內部原理並不復雜，實現的難度並不大，這裡就不過度對其實現原理加以概述。

上圖簡單的描述了用分段貝塞爾曲線來擬合橢圓並三角化成Mesh 的整個流程。最後做個科普貝塞爾曲線不是貝塞爾發明的，貝塞爾曲線也不是唯一可以用來做擬合的工控曲線。機械加工有時候要求零件表面曲率平滑，也就是曲線二階導數平滑那麼貝塞爾曲線就無能為力了。但是在圖形這個分支下貝塞爾曲線和貝塞爾曲面倒大放異彩。

建模構形

儘管通過塞爾曲線有著非常好的擬合的特性。但是在構建複雜多邊形輪廓的時候，完全通過貝塞爾曲線來擬合還是不夠方便。

如果把貝塞爾曲線構建的面所圍成的區域看成一個集合，如果可以像數學集合一樣進行“並交叉” 運算，就可以更加方便的操作二維空間。在圖形學中把這類操作看成多邊形的“布爾”運算，操作的過程可以當做多二維多邊形的建模或者叫構形。

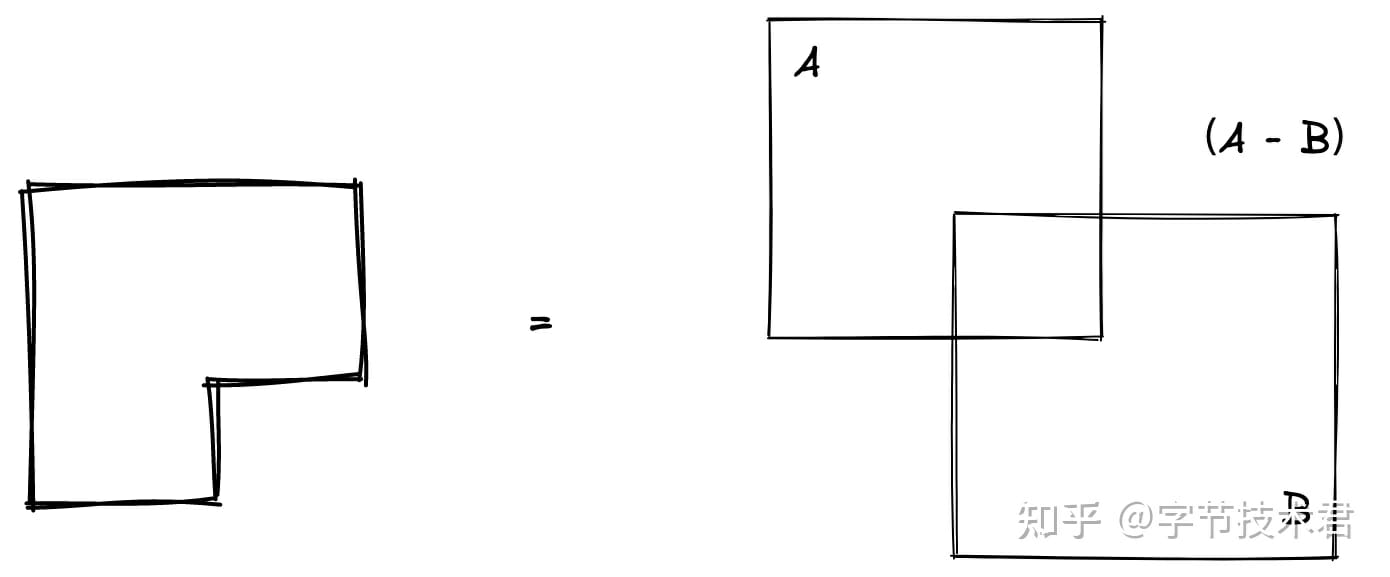
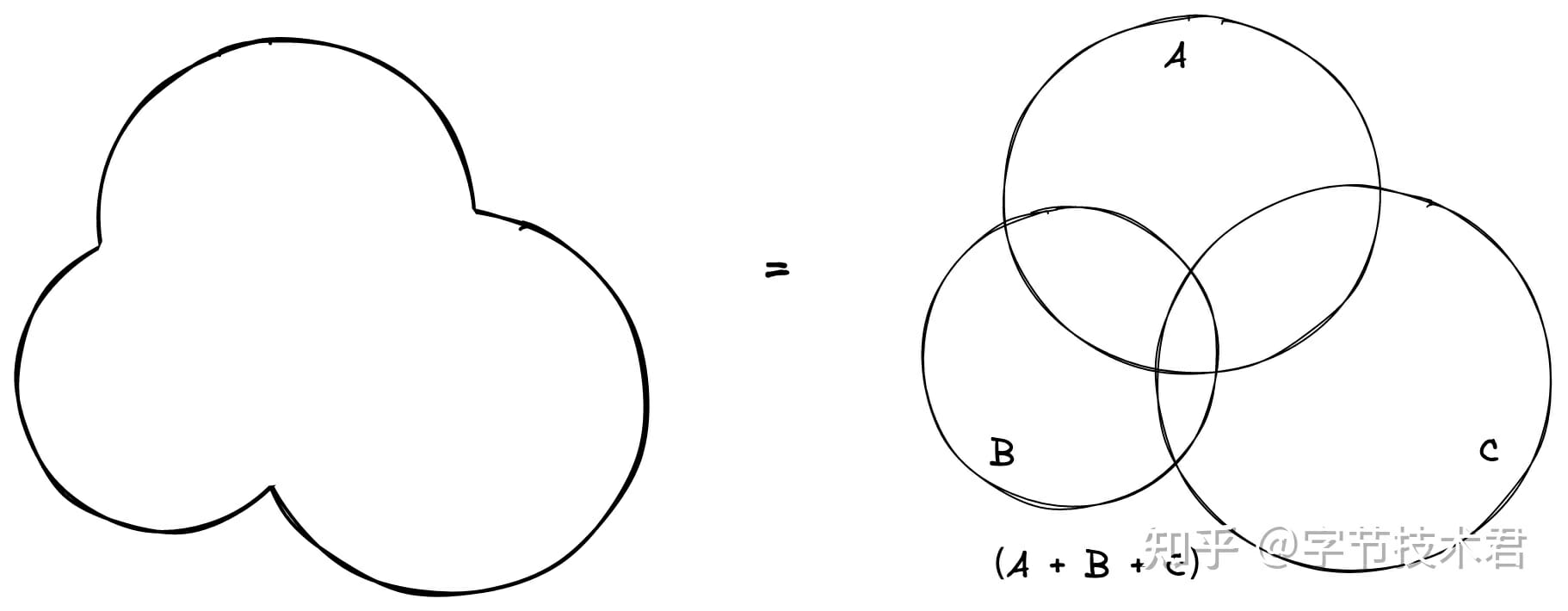
就如上圖所示，如果直接構建左側的多邊形會有一些困難。但是利用多邊形的布爾運算就比較容易了。

多邊形堆疊

一個複雜多邊形的數據定義出現了一部分區域和另一部分區域重疊，這個時候問題就開始變的異常複雜了。

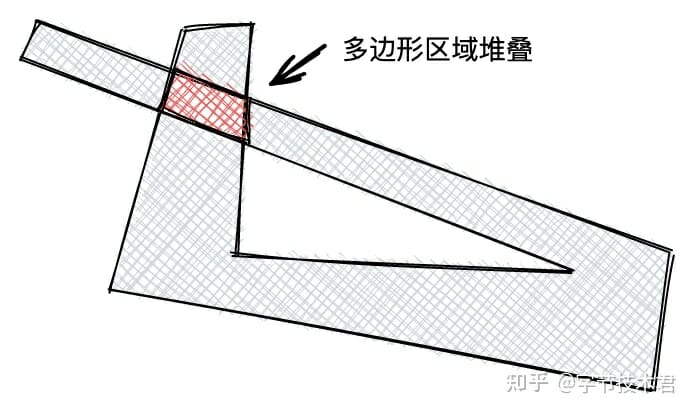
不僅僅在多邊形定義的過程中會出現多邊形區域重疊。回想一下繪製折線的過程需要對折線中的子線段進行法線平移，相當於擴大了線段描述的區域。那麼擴大了區域的同時難免會出現多邊形區域重疊。而渲染器在執行渲染前需要對多邊形進行堆疊的剔除。

布爾運算

在詳細描述如果解決多邊形堆疊問題前，先來了解一下多邊形布爾運算。 Skia 中存在對SkPath 的OP 操作就是對這個算法的實現。剔除多邊形堆疊就可以簡化成對多邊形“自己”和“自己”求並集。

這是一個古老的數學問題。不僅在圖形學中存在，在材料科學等領域都有廣泛的使用場景。數學家們為了找到這個問題的完美解，歷時長達50 年，直到1990 年Vatti bala 發表的博士畢業論文值得一提的是台灣前計算幾何協會的會長、浙江大學前數學系的主任、台灣計算幾何的泰斗直到2009 年時隔20 年後Francisco Martı´nez發表了此外從行業的經驗來看，Boost庫中的多邊形運算的子庫被認為是錯誤的實現。

由於

GPC 通用多邊形裁剪

得到GPC 的過程非常坎坷，但是算法本身卻十分容易描述。如下簡要的描述下算法的整個過程。為了簡單，採用下圖2 個凸多邊形的並集運算作為樣例。

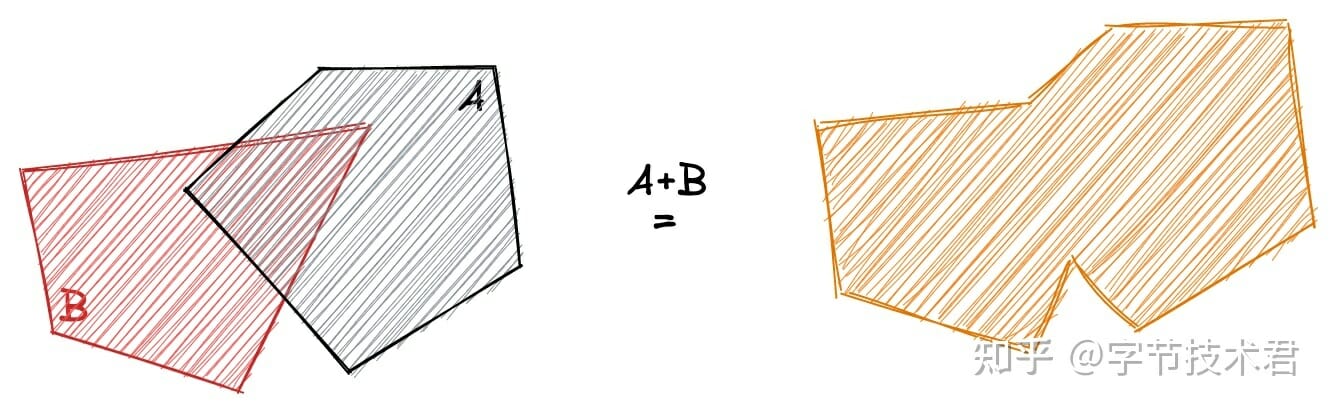
算法的關鍵在於求出邊的“交點”和“交點的進出性”。 “交點”相對比較容易理解，姑且不表。 “進出性”可以用來表達交點和對應多邊形的關係。比如下圖交點“C0” 如果從多邊形B 的B0

點出發，那麼“C0”點對於多邊形A 來說是“外部”進入到“內部”，相對應的“C0”點就是多邊形B 的出點。 “進出性”對後續的多邊形裁剪有著非常重要的意義。

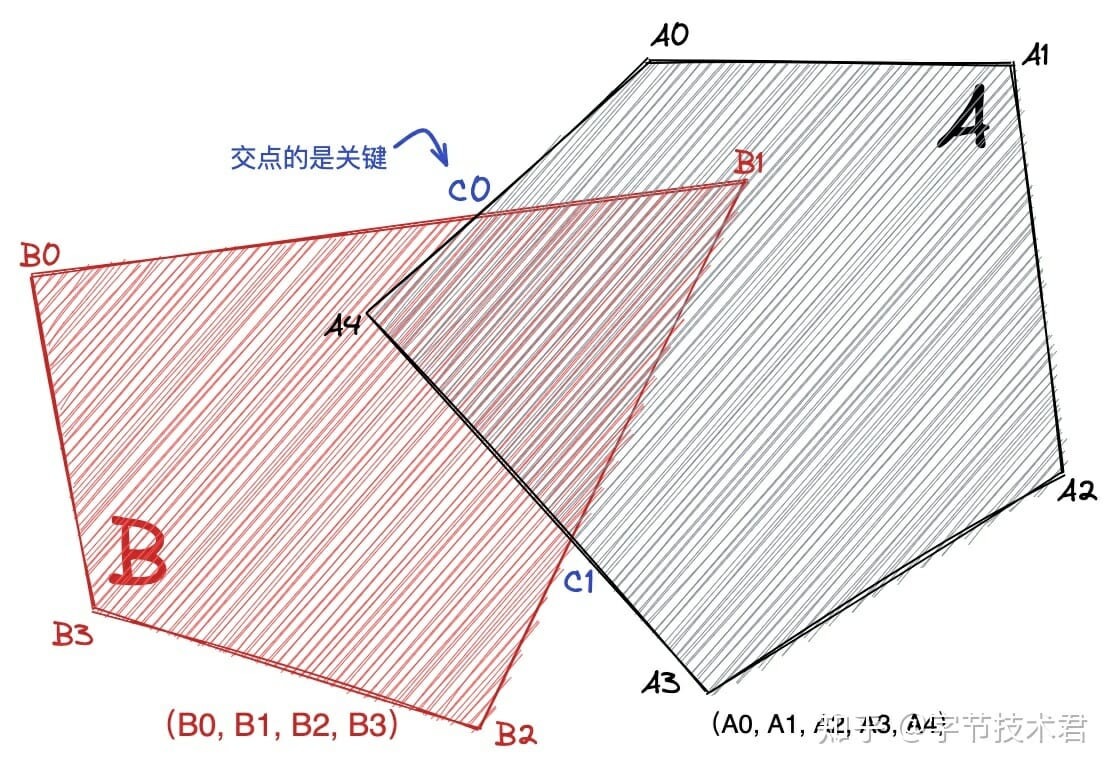
如上圖所示，多邊形A（A0,A1,A2,A3,A4）和多邊形B（B0,B1,B2,B3）。首先計算出所有的邊的交點，併計算出交點相對多邊形的進出性。然後隨機選取一個交點沿多邊形一邊進行“行進”直到遇到下一個交點。交點代表著分叉口，通過“進出性”來選取對應的路線。遞歸整個過程，直到全部的交點都被處理掉。

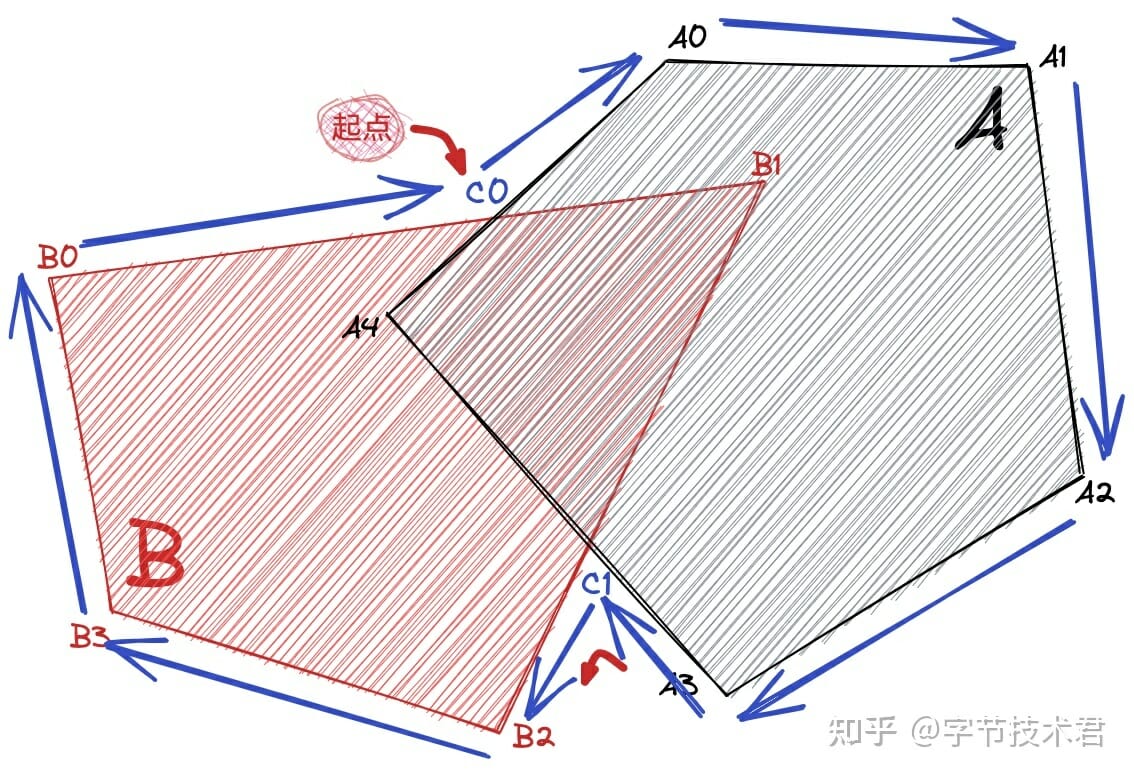
如上圖所示，“C0”作為起點開始處理，直到遇到下一個交點“C1”。考慮到“C1”的“進出性”和當前是求多邊形的“並集”，故選取“C1-B2”這條路線，直到所有的交點全部被處理。就能夠得到新的多邊形（C0,A0,A1,A2,A3,C1,B2,B3,B0），這個多邊形就是剔除了堆疊後的並集。

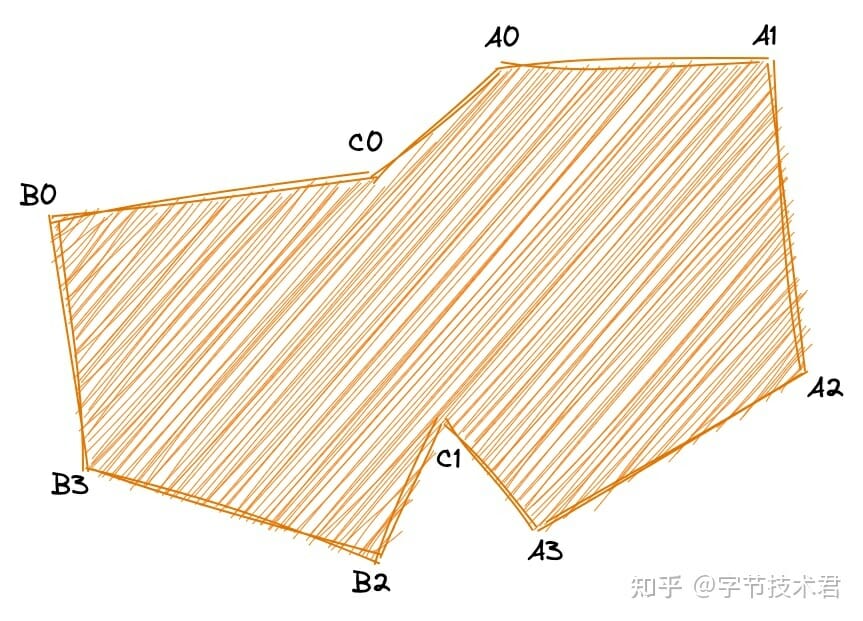
最後要解決的是如何快速求解多邊形邊的交點？尤其當多邊形異常複雜的情況下。這個可以通過線掃描配合優先隊列的方式來完成。此類算法在諸多論文中都有詳細的描述，不做詳細研究。

上圖只是描述了一個最簡單的情況，真實的情況下一般是下面這樣：

請自行腦補......

抗鋸齒

抗鋸齒本來和幾何沒有什麼關係，比如游戲中常用的抗鋸齒技術：

• SSAA
• MSAA
• FXAA

這些抗鋸齒算法在遊戲這類全畫幅處理中起到了很好地效果，但是在矢量渲染器中就不太合適，由於矢量描述多邊形擁有明確的邊界。算法只需要處理多邊形的邊界，像素的過渡中過濾所以可以在邊界進行這裡採用就拿繪製斜線的例子來說：

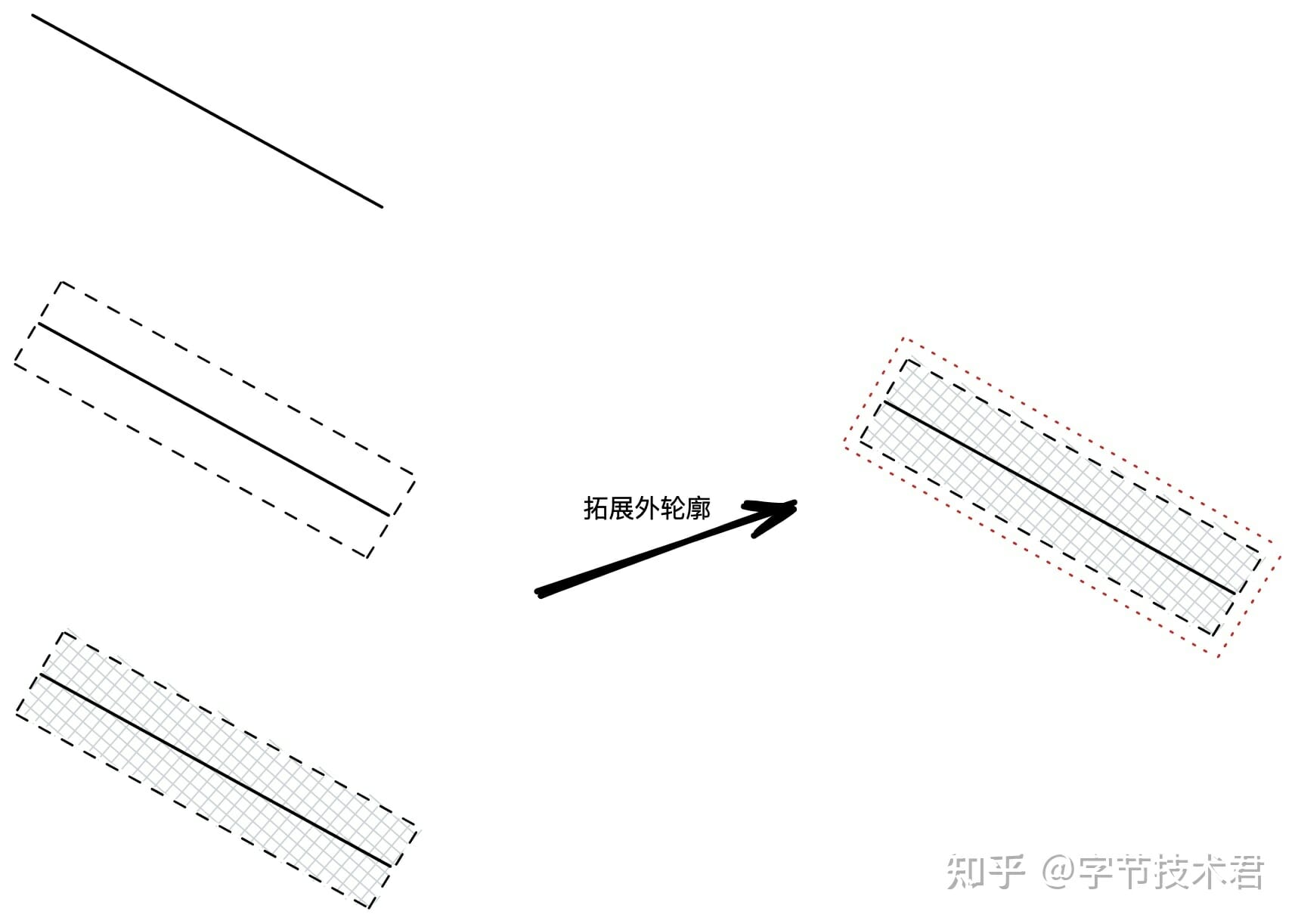
上圖前三個步驟和前文的描述沒有任何區別。在最後一步對輪廓進行了一次擴展，上圖所描述的多邊形簡單，如果對任意複雜度的多邊形執行這個過程就非常複雜了。這個過程叫“

在正確進行了外輪廓的拓展後，多邊形原本的區域被稱為“實部”，擴展出來的部分被稱為“虛部”。 “實部”依舊按照正常的渲染方式進行，此外從“實部”徑向漸變過渡到“虛部”的邊緣就可以模擬出抗鋸齒的效果。

總結

如前文所述，從分段貝塞爾曲線到二維構形，從多邊形堆疊到通用多邊形並交差。已經具備了完善的二維建模的能力，也配備了操作二維圖形的手術刀。配合三角剖分算法可以完成和GPU 的對接。

硬件加速的必要性

在計算機顯卡還沒有普及的年代，UI 依賴的矢量渲染器都是通過CPU 來實現，CPU 通過線掃描為主的一系列算法來完成像素染色。此後GPU 得到了廣為普及，由於GPU 的設計天然不適合來進行矢量渲染。故在早期嘗試使用GPU 來加速矢量渲染的嘗試中大多得到的都是負優化。

這是由於為了適應現代GPU 的運算模式，不得不在提交GPU 之前做很多預處理。包括但不限於“三角化” “特殊的邊緣抗鋸齒算法” 等等，但是在軟渲染的流程中則簡單的多。顯卡儘管可以比CPU 更快速的處理像素，但是像素的成本處理在整個過程中佔比不高。隨著顯卡速度越來越快、屏幕分辨率越來越高、顯卡的驅動標准進一步提升，這些問題得到了反轉。目前硬件加速矢量渲染已經作為重要的優化手段來使軟件界面更加流暢。

裁剪

此裁剪和幾何部分的多邊形裁剪並不一樣。特定場景下渲染器需要對渲染的結果做一些限定，比如上層的渲染邏輯只希望部分繪製的結果被用戶看到。就像Android 中父View 限定子View 的繪製不能超過父親指定的區域一樣。

硬件提供的裁剪

幾乎所有的顯卡都提供了scissor 的能力。我們在渲染前給顯卡前設置一個矩形區域，如果有像素超過這個窗口就會被顯卡丟棄掉。

但是顯卡自帶的裁剪能力要求裁剪的區域必須是一個矩形，並且這個矩形還不能夠旋轉。如果要裁剪一個奇異形狀就無能無力了，這極大限制它的使用場景。但是由硬件直接提供的能力性能非常好，對渲染無侵入。

ClipPath

Skia 中提供了一個裁剪畫布的接口ClipPath，它可以把一個貝塞爾曲線圍成的區域作為裁剪的區域。它的功能很強大，幾乎可以涵蓋全部的裁剪需求，如果不是性能太差就沒有必要提及其他的方式了。

如果需要通過ClipPath 來實現對畫布的裁剪，需要先構建一個和畫布一樣尺寸的掩碼圖。然後把區域繪製到掩碼圖上，在後續的繪製過程中要逐像素採樣掩碼圖來判斷要不要剔除。當然這個過程非常的繁重，體現在三個方面：

• 需要對區域做預處理，甚至需要做堆疊剔除
• 需要對貝塞爾曲線包圍的區域做三角化
• 需要消耗一次額外的繪製操作

正如前文描述的那樣，複雜曲線圍成的區域處理起來都非常複雜而且慢。

更快的數據結構

為了解決或者說部分解決貝塞爾曲線的複雜度帶來的性能損耗。可以使用多個矩形來表示一個複雜區域，但是要求矩形之間不能存在堆疊。下圖描述瞭如何剔除矩形之間的堆疊，只需要執行一次線掃描算法即可。

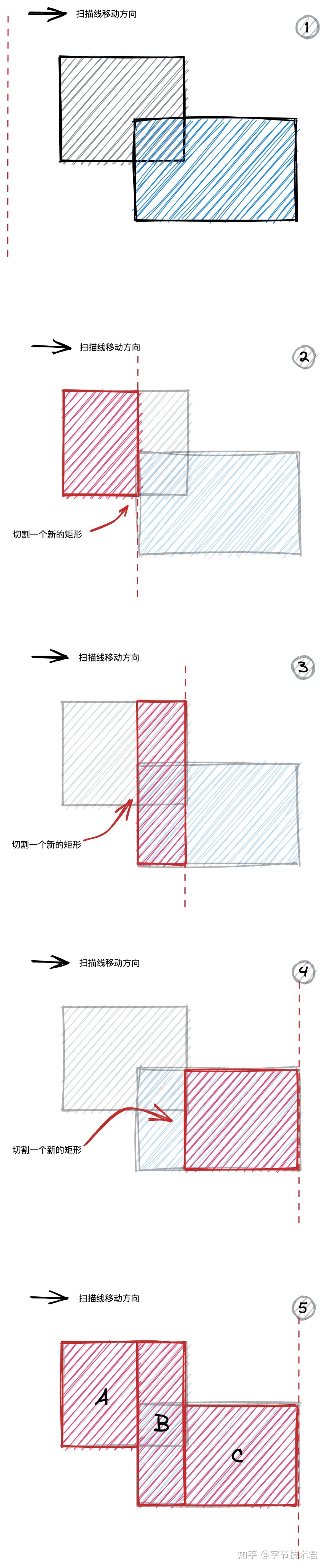
同樣矩形非常容易就可以剖分成三角形，並不需要使用複雜的三角剖分的算法。所以可以快速構建對二維區域的描述。同樣基於“矩形集合”的二維區域描述非常容易構建出並交差等運算。而且相關的碰撞檢測算法也非常容易實現，但是對於需要使用曲線包圍的區域就顯的比較乏力了。

Skia 中使用SkRegion 這個數據結構來對這個算法進行描述。

SDF 快速剔除

SDF（Signed Distance Field，有向距離場），這裡用了一種模擬SDF 的方法來進行快速的裁剪。它發生在光柵化後像素處理的最後階段。

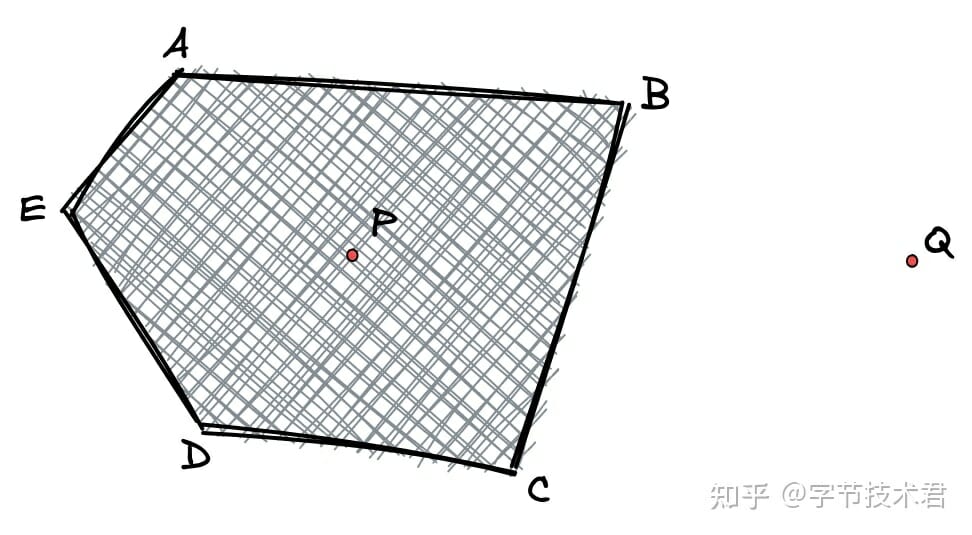
比如上圖中像素P 和像素Q，如果需要保留多邊形（A，B，C，D，E）區域。那麼就要找到一個辦法來區分像素P和Q 誰落在多邊形內，誰落在多邊形外。這不是一個很麻煩的事。

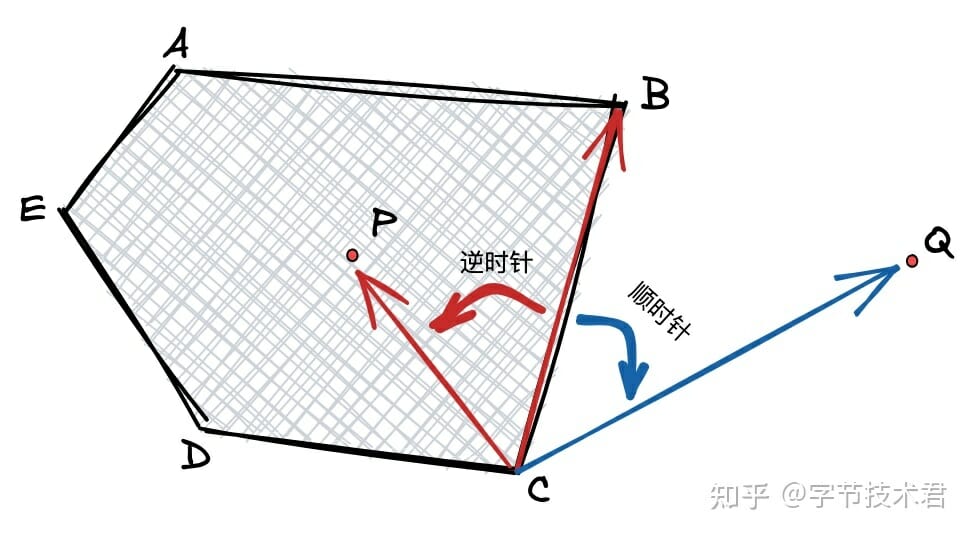
如上圖所示，從多邊形任意一個點進行“行進”，圖中從C 點開始。那麼向量CB 需要逆時針旋轉才可能和向量CP 重合，也就是P 點在向量CB 的左側，相反像素Q 在向量CB 的右側。循環一周會發現點P 永遠在左側，而Q 則有時候在左側有時候在右側。至於左右可以通過向量幾何的叉積的正負來判斷。通過這個特性可以判斷像素是不是處於多邊形的包圍中。算法中可以通過這個原理構建SDF的核函數。理論上只能對凸多邊形有效果，其他多邊形需要轉化成多個凸多邊形後依次加以判斷（實際上還存在其他問題）。在判斷像素的時候同時需要找到像素距離每個邊的最短距離，通過這個距離可以控制邊緣的一些策略用來抗鋸齒。

Skia 中並未暴露SDF 相關的策略接口，但是在內核代碼中存在類似的實現。

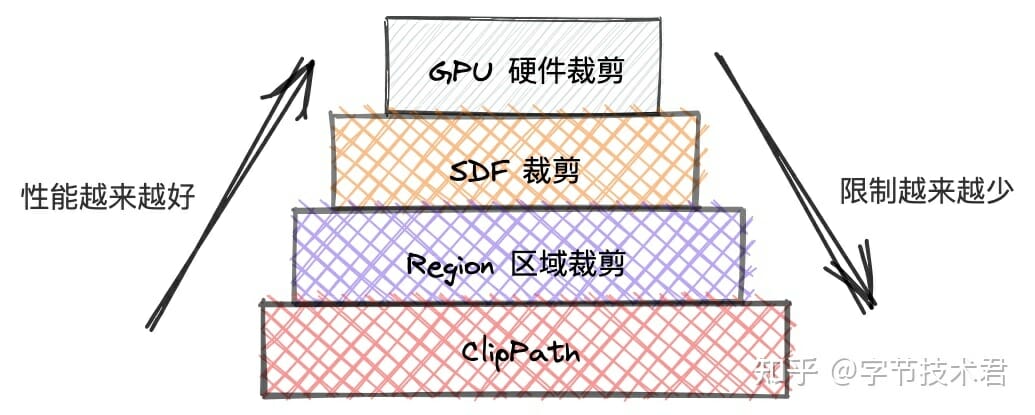
上文描述了幾個典型的裁剪方式。理論上需要上層業務進行合理的選擇，用以達到最佳的性能，而不是無腦的ClipPath。

和Skia 的差異

SaveLayers

暫時不覺得需要提供SaveLayers 這類接口。

CPU Backend 渲染器

只支持硬件加速渲染，盡可能的多支持不同的硬件。不考慮CPU Backend，對普眾的消費電子設備顯卡應該和CPU 一樣是標配。不存在GPU 的設備不在考慮範圍內。

為什麼體積會小這麼多

主要由一下幾個因素

• 我們實現的渲染器不支持CPU軟渲染策略，一些都是為了硬件加速設計的，更加簡潔。
• 作為Shader處理的邏輯，核心的編譯器相關模塊都是離線實現。同樣的Skia的SKSL編譯器需要內置到Skia的核心邏輯中難以剝離。
• 由於Skia的歷史非常悠久，存在相當多的legacy性質的代碼和模塊。

總結

至此整個矢量渲染器的核心技術就已經描述完畢。每個部分單獨實現難度並不大，但是集合起來構建一個完備的項目還是太“頂”了。如果你也想實現一個類似的渲染器，那麼祝你好運。

關於渲染器的未來使用場景

跨平台

這個方向毋庸置疑，未來類似Flutter 這樣的跨多端的會慢慢變成主流（多年前筆者從事Windows 開發，就是先用系統的渲染器繪製一套UI 體系，然後在上面做各種業務。Flutter 在移動端算一個新東西，但是業界早有類似的解決方案），那麼構建適合自己業務的渲染引擎非常有必要，也是技術實力的體現。

Mini 瀏覽器

隨著前端的敏捷的開發方式慢慢在整個行業得到接受，國內有眾多嘗試在系統原生組件或者Flutter 上構建類似瀏覽器的邏輯（遠不如瀏覽器那麼複雜）。我把這類項目稱為Mini 瀏覽器項目，那麼渲染器可以最大化減少包體積，提高渲染性能。

天下沒有免費的午餐，沒有哪一個硬件渲染器能夠保證，隨意使用其API 就能得到好的性能。 Flutter 本身也因為過多使用Skia 的ClipPath 和SaveLayers 導致性能低下。對渲染本身足夠理解、對硬件的足夠理解，知己知彼才能做到最好。

混合渲染

縱觀全文，我都致力於把二維渲染實時轉化成由三角形構成的Mesh。那麼3D 遊戲為什麼可以在渲染複雜的場景下提供好的性能？原因在於3D 遊戲中使用的3D 模型大多都是通過“3DMax” “Maya” “Blender”這裡建模工具離線構建的。

從三角形的Mesh 角度來說，2D 和3D 沒有本質區別，所以可以混合到一起渲染。這會帶來一些新的原來不具備的特性。移動設備時至今日運算能力已經很強了，但是交互方式卻沒有大的變化，隨著混合模式下的渲染會帶來更加新穎的體驗的交互模式。

作者介紹

陳國棟， 主要從事多端跨平台、計算機圖形學、編譯器、高並發、分佈式共識和一致性的研究和實踐。其所在的團隊對外負責的技術產品有Lynx（移動端動態化跨平台引擎）、JavaScript虛擬機、瀏覽器內核、自渲染框架內核等。歡迎有意向在以上幾個方向參與研究和研發的同學加入我們。