新的一年，先給大家整理分享一個簡單而又重要的知識點：時間複雜度和空間複雜度。因為在前幾篇文章中，提到了時間複雜度，也許有些小伙伴還不清楚。

先給大家出個思考題，計算：sum = 1+2+3+...+n ，計算sum 的值。

為什麼需要復雜度分析

• 學習數據和算法就是為了解“快”和“省”的問題，也就是如何設計你的代碼才能使運算效率更快，佔用空間更小。那如何來計算代碼執行效率呢？這裡就會用到復雜度分析。
• 雖然我們可以用代碼準確的計算出執行時間，但是這也會有很多局限性。
• 數據規模的不同會直接影響到測試結果。比如說同一個排序算法，排序順序不一樣，那麼最後的計算效率的結果也會不一樣；如果恰好已經是排序好的了數組，那麼執行時間就會更短。又比如說如果數據規模比較小的話，測試結果可能也無法反應算法的性能。
• 測試的環境不同也會影響到測試結果。比如說同一套代碼分別在i3 和i7 處理器上進行測試，那麼i7 上的測試時間肯定會比i3 上的短。

所以需要一個不用準確的測試結果來衡量，就可以粗略地估計代碼執行時間的方法。這就是複雜度分析。

大O 複雜度表示法

以一個例子開始，請估算下面代碼的執行時間

function total(n) { // 1 var sum = 0; // 2 for (var i = 0; i < n; i++) { // 3 sum += i; // 4 } //5 } //6

我們假設每行代碼執行的時間都一樣，記做t，那麼上面的函數中的第2 行需要1 個t 的時間，第3 行和第4 行分別需要n 個t 的時間，那麼這段代碼總的執行時間為(2n+1)*t。

那麼按照上面的分析方法，請估算下面代碼的執行時間

function total(n) { // 1 var sum = 0; // 2 for (var i = 0; i < n; i++) { // 3 for (var j = 0; j < n; j++) { // 4 sum = sum + i + j; // 5 } } }

第2 行需要一個t 的時間，第3 行需要n 個t 的時間，第4 行和第5 行分別需要n2 個的時間，那麼這段代碼總的執行時間為(2n2+n+1)* t 的時間。

從數學角度來看，我們可以得出個規律：代碼的總執行時間T(n) 與每行代碼的執行次數成正比

T(n) = O(f(n))

在這個公式中，T(n) 表示代碼的執行時間；n 表示數據規模的大小；f(n) 表示每行代碼執行的次數總和；O 表示代碼的執行時間T(n) 與f(n)表達式成正比。

所以上邊兩個函數的執行時間可以標記為T(n) = O(2n+1) 和T(n) = O(2n2+n+1)。這就是大O時間複雜度表示法，它不代表代碼真正的執行時間，而是表示代碼隨數據規模增長的變化趨勢，簡稱時間複雜度。

而且當n 很大時，我們可以忽略常數項，只保留一個最大量級即可。所以上邊的代碼執行時間可以簡單標記為T(n) = O(n) 和T(n) = O(n2)。

時間複雜度分析

那如何分析一段代碼的時間複雜度呢，可以利用下面的幾個方法

1.只關注循環執行次數最多的一段代碼

我們在分析一段代碼的時間複雜度時，我們只要關注循環次數最多的那一段代碼就ok 了。比如說在第一段代碼中

function total(n) { // 1 var sum = 0; // 2 for (var i = 0; i < n; i++) { // 3 sum += i; // 4 } //5 } //6

只有第3 行和第4 行是執行次數最多的，分別執行了n 次，那麼忽略常數項，所以此段代碼的時間複雜度就是O(n)。

2.加法法則：總複雜度等於量級最大的那段代碼的複雜度。

比如說，看下面這段代碼的時間複雜度。

function total(n) { // 第一个for 循环var sum1 = 0; for (var i = 0; i < n; i++) { for (var j = 0; j < n; j++) { sum1 = sum1 + i + j; } } // 第二个for 循环var sum2 = 0; for(var i=0;i<1000;i++) { sum2 = sum2 + i; } // 第三个for 循环var sum3 = 0; for (var i = 0; i < n; i++) { sum3 = sum3 + i; } }

我們先分別分析每段for 循環的時間複雜度，再取他們中最大的量級來作為整段代碼的時間複雜度。

第一段for 循環的時間複雜度為O(n2)。

第二段for 循環執行了1000 次，是個常數量級，儘管對代碼的執行時間會有影響，但是當n 無限大的時候，就可以忽略。因為它本身對增長趨勢沒有影響，所以這段代碼的時間複雜度可以忽略。

第三段for 循環的時間複雜度為O(n)。

總上，取最大量級，所以整段代碼的時間複雜度為O(n2)。

3.乘法法則：嵌套代碼的複雜度等於嵌套內外代碼複雜度的乘積。

比如說，看下面這段代碼的時間複雜度

function f(i) { var sum = 0; for (var j = 0; j < i; j++) { sum += i; } return sum; } function total(n) { var res = 0; for (var i = 0; i < n; i++) { res = res + f(i); // 调用f 函数} }

單獨看total 函數的時間複雜度就是為T1(n)=O(n)，但是考慮到f 函數的時間複雜度也為T2(n)=O(n)。所以整段代碼的時間複雜度為T(n) = T1(n) * T2(n) = O(n*n)=O(n2)。

幾種常見的時間複雜度分析

只看最高量級的複雜度

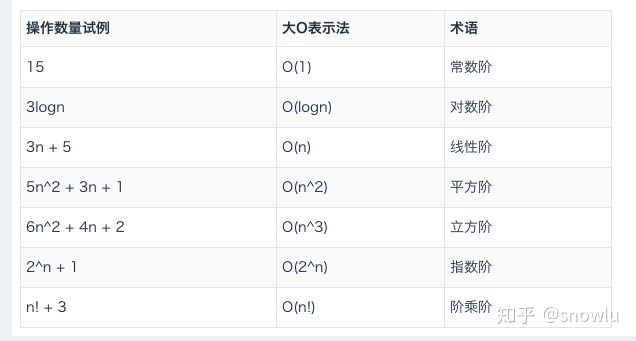
如上圖可以粗略的分為兩類，多項式量級和非多項式量級。其中，非多項式量級只有兩個：O(2n)和O(n!)對應的增長率如下圖所示

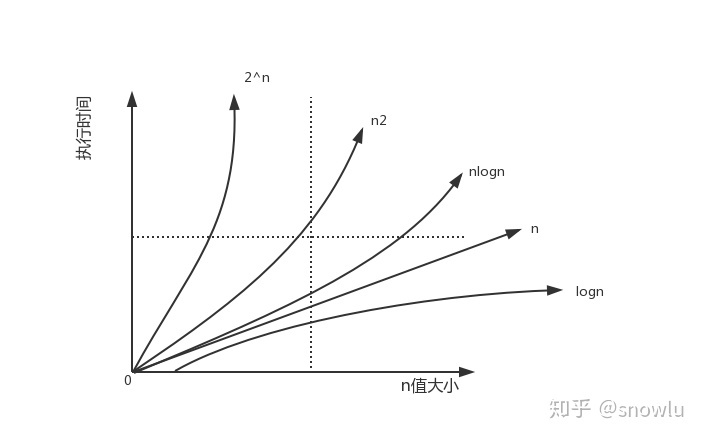
當數據規模n增長時，非多項式量級的執行時間就會急劇增加，所以，非多項式量級的代碼算法是非常低效的算法。

1. O(1)

O(1) 只是常量級時間複雜度表示法，並不是代碼只有一行，比如說下面這段代碼

function total() { var sum = 0; for(var i=0;i<100;i++) { sum += i; } }

雖然有這麼多行，即使for 循環執行了100 次，但是代碼的執行時間不隨n 的增大而增長，所以這樣的代碼複雜度就為O(1)。

2. O(logn)、O(nlogn)

對數階時間複雜度的常見代碼如下

function total1(n) { var sum = 0; var i = 1; while (i <= n) { sum += i; i = i * 2; } } function total2(n) { var sum = 0; for (var i = 1; i <= n; i = i * 2) { sum += i; } }

上面兩個函數都有一個相同點，變量i 從1 開始取值，每循環一次乘以2，當大於n 時，循環結束。實際上，i 的取值就是一個等比數列，就像下面這樣

20 21 22 ... 2k... 2x =n;

所以只要知道x 的值，就可以知道這兩個函數的執行次數了。那由2x = n 可以得出x = log2n，所以這兩個函數的時間複雜度為O(log2n)。

再看下面兩個函數的時間複雜度

function total1(n) { var sum = 0; var i = 1; while (i <= n) { sum += i; i = i * 3; } } function total2(n) { var sum = 0; for (var i = 1; i <= n; i = i * 3) { sum += i; } }

由上可以得知，這兩個函數的時間複雜度為O(log3n) 。

由於我們可以忽略常數，也可以忽略對數中的底數，所以在對數階複雜度中，統一表示為O(logn)；那O(nlogn) 的含義就很明確了，時間複雜度為O( logn) 的代碼執行了n 次。

3. O(m+n)、O(m*n)

再來看一段特殊的代碼時間複雜度，比如說

function total(m,n) { var sum1 = 0; for (var i = 0; i < n; i++) { sum1 += i; } var sum2 = 0; for (var i = 0; i < m; i++) { sum2 += i; } return sum1 + sum2; }

因為我們無法評估m 和n 誰的量級比較大，所以就不能忽略掉其中一個，這個函數的複雜度是有兩個數據的量級來決定的，所以此函數的時間複雜度為O(m +n)；那麼O(m*n) 的時間複雜度類似。

空間複雜度分析

空間複雜度的話和時間複雜度類似推算即可。所謂空間複雜度就是表示算法的存儲空間和數據規模之間的關係。

比如說分析下面代碼的空間複雜度：

function initArr(n) { var arr = []; for (var i = 0; i < n; i++) { arr[i] = i; } }

根據時間複雜度的推算，忽略掉常數量級，每次數組賦值都會申請一個空間存儲變量，所以此函數的空間複雜度為O(n)。

常見的空間複雜度只有O(1)、O(n)、O(n2)。其他的話很少會用到。

思考題解答

現在我們回到開始的思考題上，代碼實現很簡單：

function total(n) { var sum = 0; for (var i = 1; i <= n; i++) { sum += i; } return sum; }

此函數的時間複雜度你現在應該很容易就能看出來了，為O(n)。

我覺得這個時間複雜度有點高了，我想要O(1) 的時間複雜度函數來實現這個算法，可以嗎？

可以的，小數學神通高斯教會我們一招，如下

function total(n) { var sum = n*(n+1)/2 return sum; }

此函數的時間複雜度僅僅為O(1)，在數據規模比較龐大的時候，下面的函數是不是明顯比上面的函數運算效率更高呢。

總結

複雜度也叫漸進複雜度，包括時間複雜度和空間複雜度，一個表示執行的快慢，一個表示內存的消耗，用來分析算法執行效率與數據規模之間的增長關係，可以粗略的表示，越高階複雜度的算法，執行效率越低。

學習了複雜度分析後，是不是能避免寫出效率低的代碼呢？來給你的代碼做個分析吧。

重點

如果有錯誤或者錯別字，還請給我留言指出，謝謝。

我們下期見。